原创文章,转载、引用请注明出处!
2019-05-20更新专题设计内容。
目标任务
要求
完成以下描述赋值语句的 LL(1)文法的递归下降分析程序
G[A]: S→V=E
E→TE’
E’→ATE’|ε
T→FT’
T’→MFT’|ε
F→ (E)|i
A→+|-
M→*|/
V→i
设计说明
终结符号i为用户定义的简单变量,即标识符的定义。
设计要求
(1)输入串应是词法分析的输出二元式序列,即某算术表达式“专题1”的输出结果,输出为输入串是否为该文法定义的算术表达式的判断结果;
(2)递归下降分析程序应能发现简单的语法错误;
(3)设计两个测试用例(尽可能完备,正确和出错),并给出测试结果;
(4)选做:如有可能,考虑如何用文法描述C语言的if语句,使整个文法仍然为LL(1)文法,并使得你的递归下降程序可以分析赋值语句和if语句。
解答
递归下降分析
在不含左递归和每个非终结符的所有的首符集都两两不想交的条件下。我们就可以构造一个不带回溯的的自上而下的分析程序。该程序是由一组递归过程组成的。每个过程对应文法的一个非终结符。这种语法分析的方法称为文法递归下降分析法。
当一个文法满足LL(1)条件时,我们就可以为它构造一个不带回溯的自上而下分析程序,这个分析程序是由一组递归过程组成的,每个过程对应文法的一个非终结符,这样的一个分析程序称为递归下降分析器。
相比于词法分析器,构造语法分析器的方法有很多,而递归下降的方法是较为常见和简单的一种。
递归下降分析对于文法是有一定要求的:文法必须为LL(1)文法。而LL(1)文法的要求是:一为文法不含有左递归,另一为文法不含有回溯。如果存在上述情况,需要先对文法进行处理,在消除这两种情况之后方可对文法进行递归下降分析。
设计思想
递归下降分析器的构造方法非常简单,就是为每一个非终结符写一个递归函数,函数中对该终结符可能转换成的所有情况的第一个token进行判断,做出对应的处理。
需要注意的是,在进行递归下降分析之前需要对不是LL(1)的文法进行处理。
为了方便程序的编写,可先将文法转换为流程图。

左递归和回溯的消除
由于所给的文法为标准的LL(1)文法,这一步可省略。
将文法转换为流程图
对于所给的9条产生式,做如下流程图的转换:
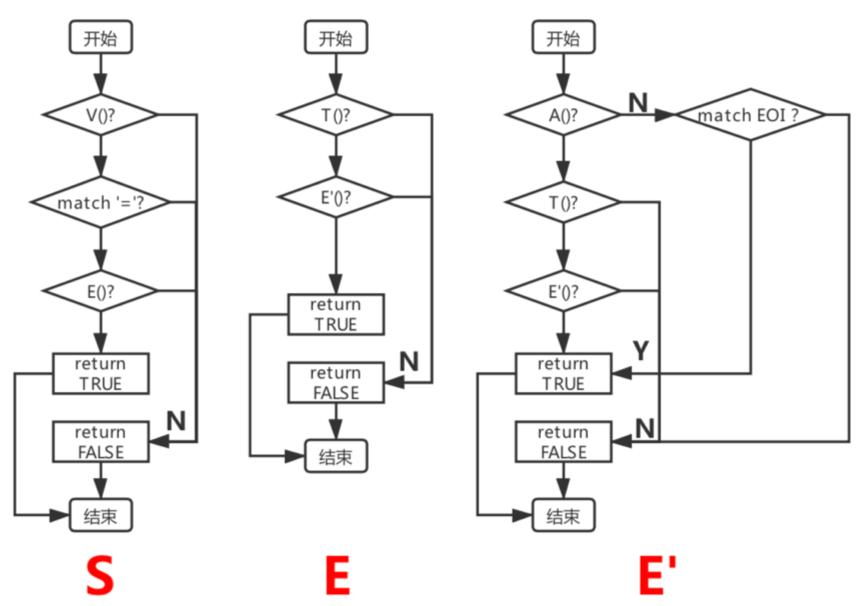
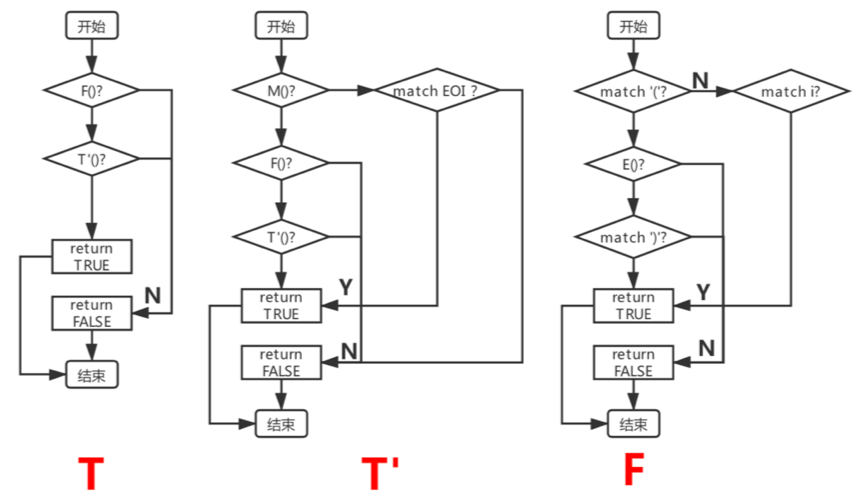
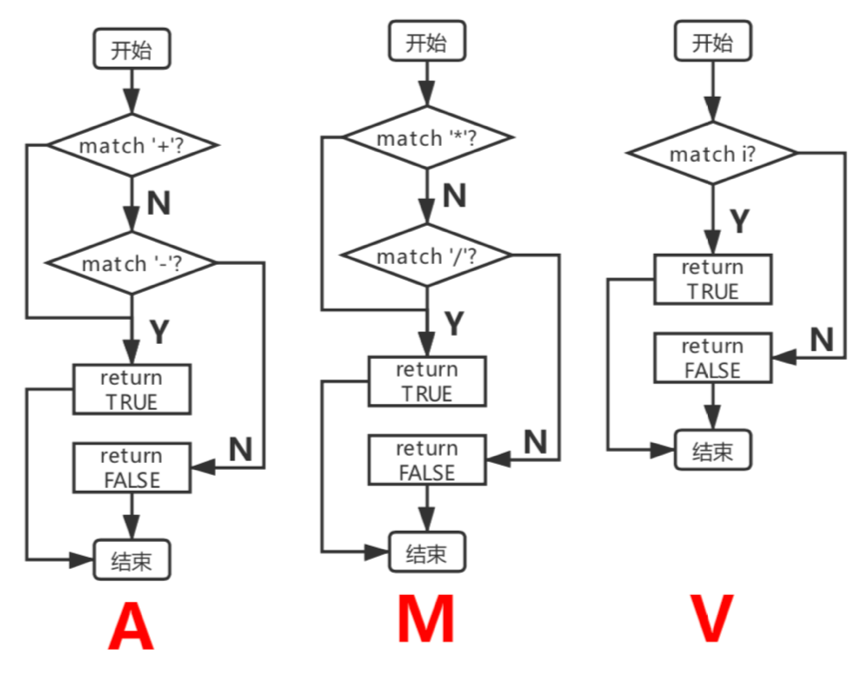
上述函数中,“match“是对单个特定终结符号的匹配,”match EOI“代表匹配“ε”。
文件结构及函数简介
本专题大部分文件和功能函数与上一专题同名,具体的文件结构和功能函数简介见《编译原理:词法分析程序》。
算法函数命名同产生式的左部,且全部为bool类型。
例如,对于产生式S→V=E,对应的函数为bool S()。
代码分析
详细的主函数流程如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
int main(int argc, const char * argv[]) {
initAll();
readFile_Result();
readFile_Identifier();
getPureMorpheme();
printMorphemeInfo();
if(judge()){
cout<<"匹配成功!"<<endl;
}else{
cout<<"匹配失败!"<<endl;
printError();
}
return 0;
}
|
由于本专题要求的输入是上一个专题输出的词素结果二元组和标识符信息,则需要从上一专题的输出文件中读取信息,并将信息过滤为我们需要的词素,以此作语法分析:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
void readFile_Identifier(){
FILE *fp;
fp=fopen(FileName_Write_Identifier,"r");
if(fp==NULL){
cout<<"SYSTEM ERROR(readFile_Identifier)"<<endl;
exit(0);
}
int i=0;
char temp[100]="\0";
while(!feof(fp)){
fgets(temp,1000,fp);
identifier[i]=temp;
identifier[i].pop_back();
i++;
}
idCounter=i;
fclose(fp);
}
void readFile_Result(){
FILE *fp;
fp=fopen(FileName_Write_Result,"r");
if(fp==NULL){
cout<<"SYSTEM ERROR(readFile_Result)"<<endl;
exit(0);
}
int i=0;
char temp[100]="\0";
while(!feof(fp)){
fgets(temp,1000,fp);
morpheme[i]=temp;
i++;
}
morphemeCounter=i;
fclose(fp);
}
|
读取完词素二元组文件之后,需要对读取的内容进行过滤, 使得容器中只含词素本身,具体做法为去除从左括号(含)开始到词素本身以及词素之后的右括号。
在上述准备工作做完后,调用判断函数judge()进行判断即可。judge()函数的功能就是调用文法开始符号所对应的S()函数。
对于S()这样的算法函数,具体的做法是使用条件判断语句对应流程图做好判断即可。
以S()函数为例,递归下降分析程序对于产生式判断的基本流程如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
bool S(){
if(V()){
if(!morpheme[pMorpheme].compare("=")){
pMorpheme+=1;
if(E()){
return true;
}else{
return false;
}
}else{
return false;
}
}else{
return false;}}
|
结果测试
首先依据所给文法写出一正确的语句:
var_a=(var_b+var_c*var_d)/(var_e-var_f)-var_g
将此表达式写入专题1中的SourceProgram.txt文件:
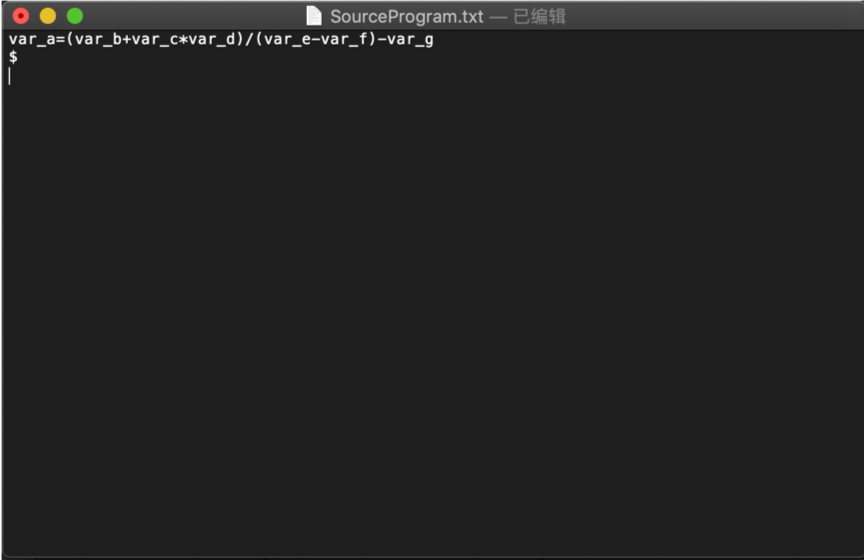
运行专题1程序:
查看标识符文件Identifier.txt:
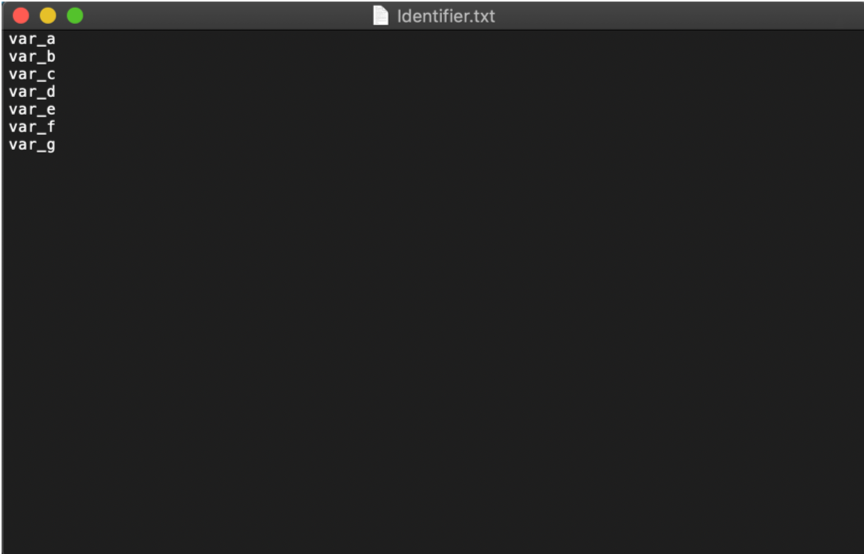
查看词素二元组文件ResultofLexicalAnalysis.txt:
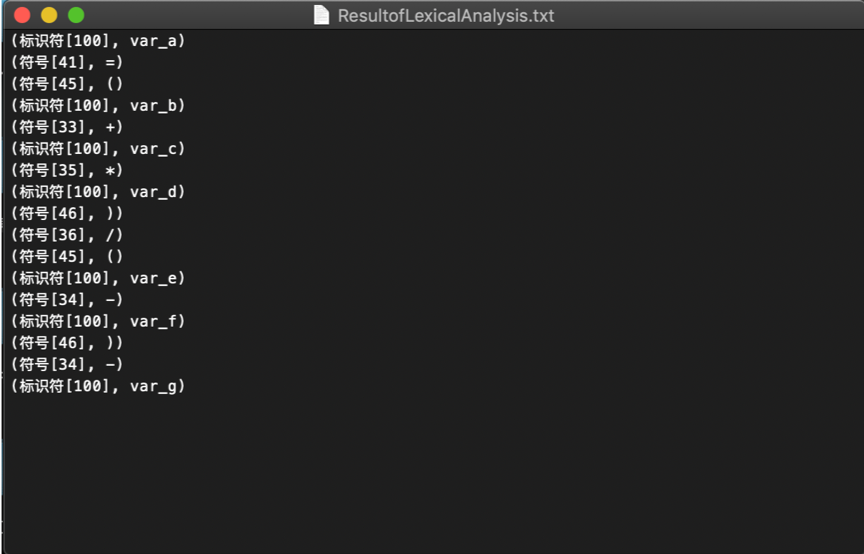
可以看到对于专题1来说,上述语句是符合要求的。
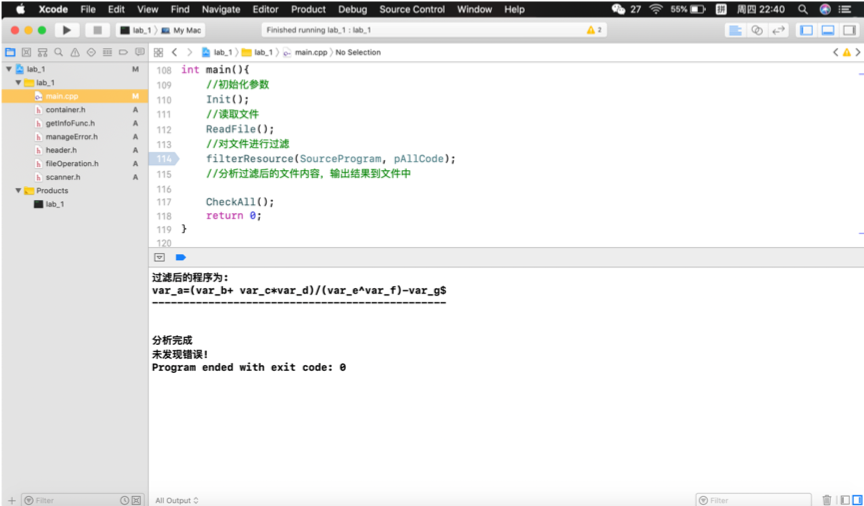
接下来运行本专题的递归下降判断程序:
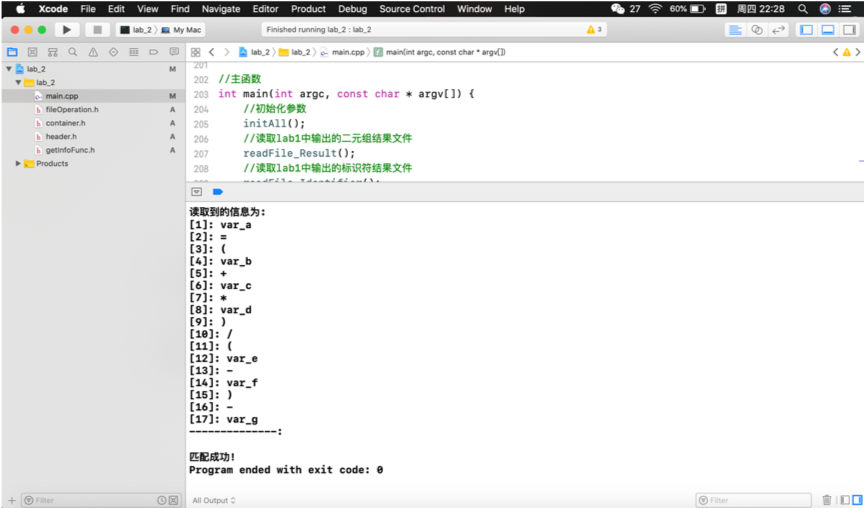
上述测试证明了两个程序可按设计本意顺利完成各项功能。
接下来,修改我们所给出的正确的语句,使它变得”错误”。当然这里所说的错误指的是在本专题的情景下是错误的。这些语句无论如何修改,都必须符合专题1的情景。
(1)var_a+var_error=(var_b+var_c*var_d)/(var_e-var_f)-var_g
(2)var_a=(var_b+233*var_d)/(var_e-var_f)-var_g
(3)var_a=(var_b+ var_c*var_d)/(var_e^var_f)-var_g
标示出来的是我们添加的错误。
分别对如上情形进行测试:
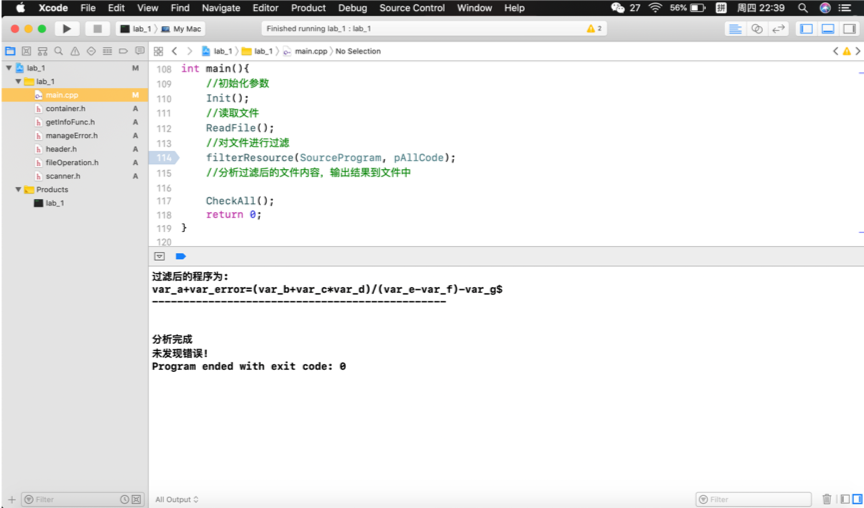
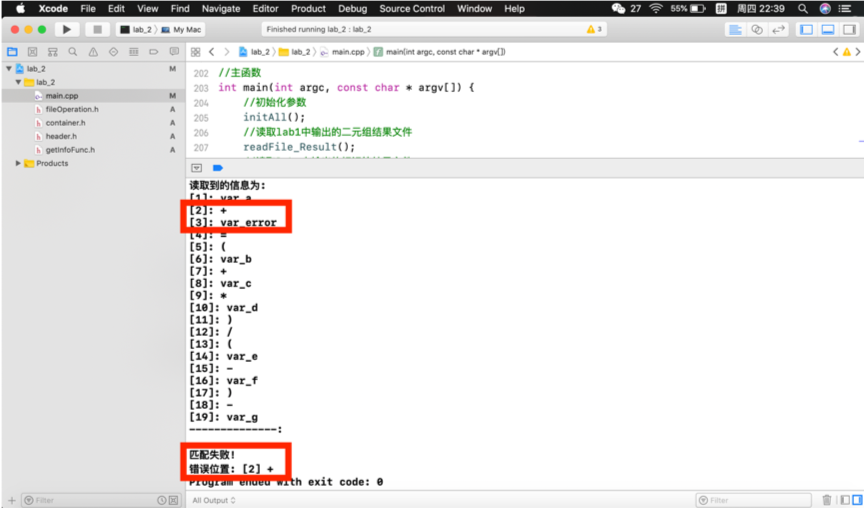
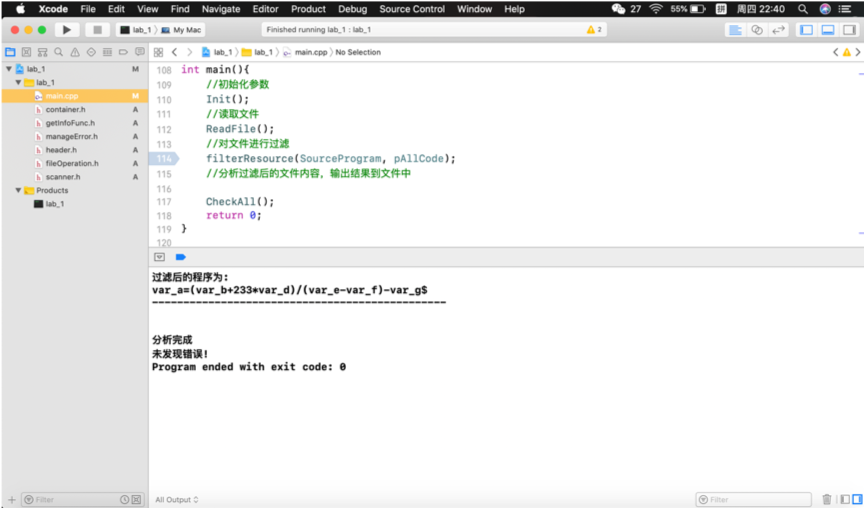
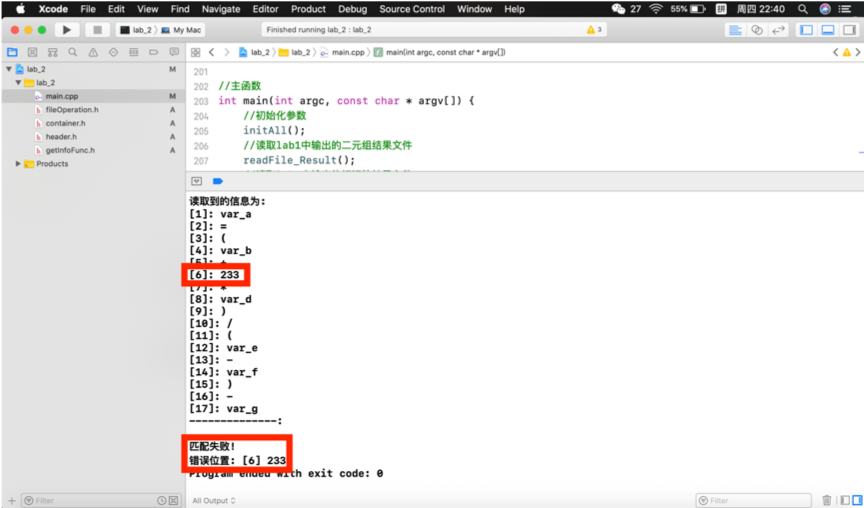
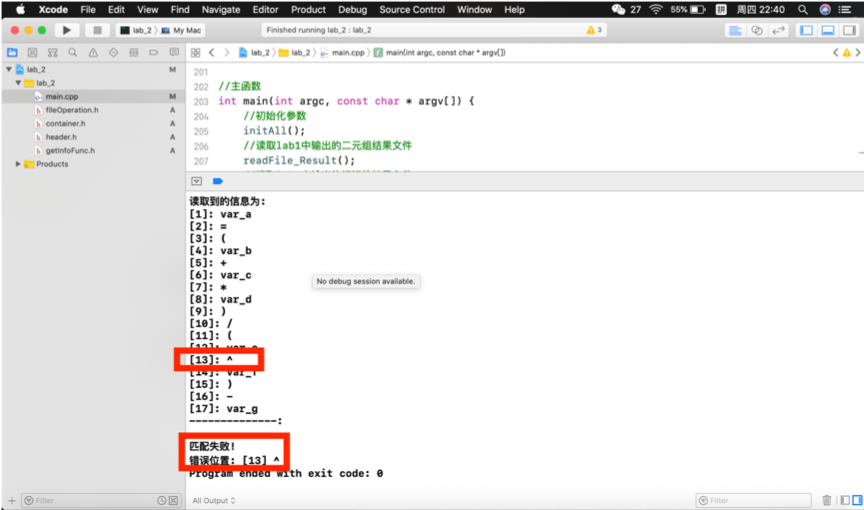
根据上述结果可以看出,本程序可以实现所给LL(1)文法的递归下降分析,并能指出具体错误的位置。
原例题
题目
某将如下文法 G[<程序>],改写为 LL(1)文法,画出递归下降分析程序框图。
<程序>→begin <语句> end
<语句>→<赋值语句>│<条件语句>
<赋值语句>→<变量>:=<表达式>
<条件语句>→if <表达式> then <语句>
<表达式>→<表达式>+<变量>│<变量>
<变量>→i
递归下降分析实现原理
若要使用递归下降分析,首先得将文法变为LL(1)文法。
将文法变为LL(1)文法需要两个步骤:检查是否有左递归并消除、检查是否有回溯并消除。
实现
文法处理
左递归
经过检查发现,该文法中含有如下左递归:
消除左递归步骤如下:
1
2
3
4
5
| <表达式> → <表达式> + <变量> │ <变量>
<表达式> → <变量> { + <变量> }
//令 { + <变量> } = <表达式>'
<表达式> → <变量> <表达式>'
<表达式>' → + <变量> <表达式>' | ξ
|
回溯
经过检查发现,该文法无回溯,可省略此步骤。
按照处理后的文法画出流程图
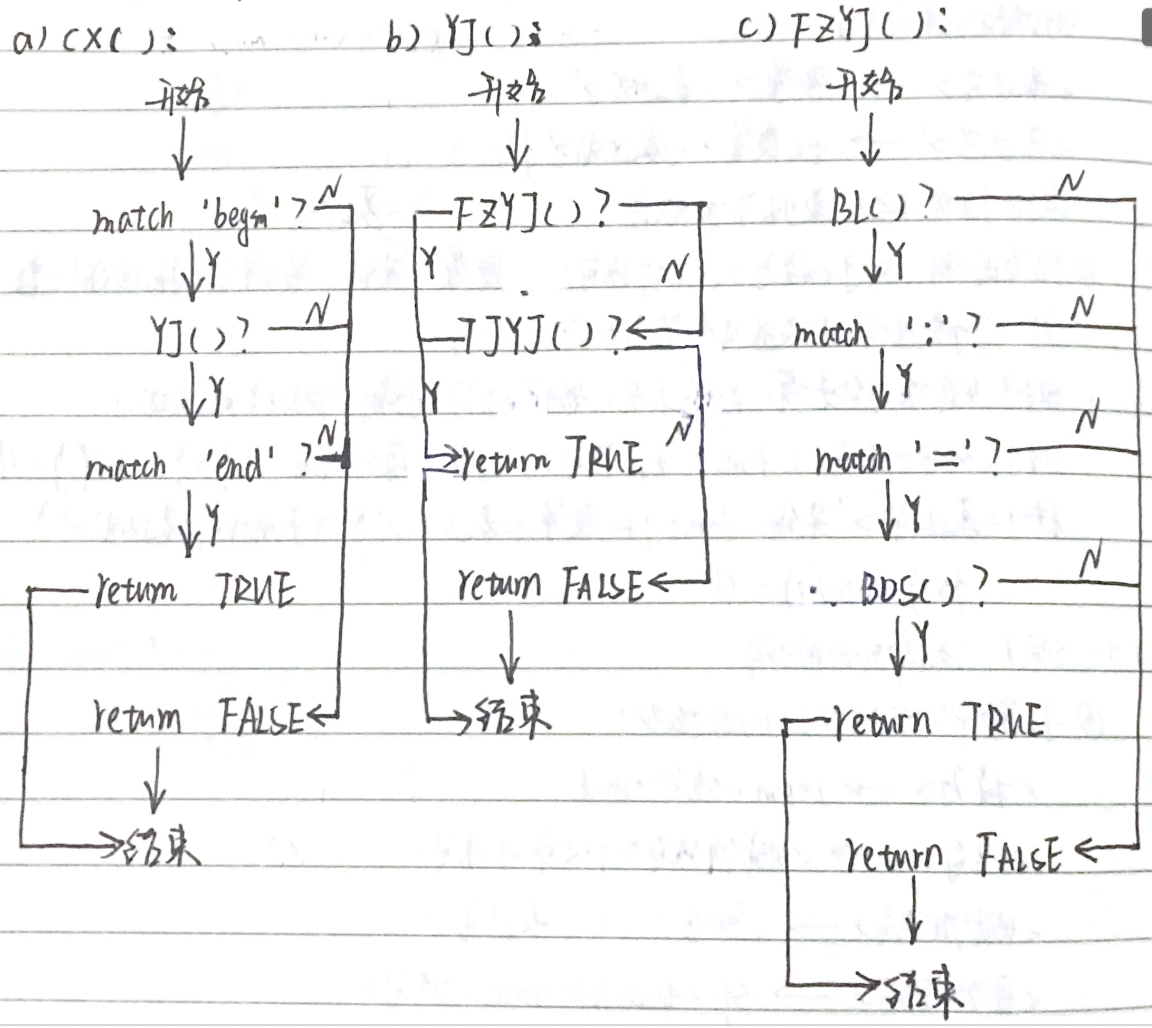

按照流程图编写代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
| #include <stdio.h>
#include <iostream>
#include <string>
using namespace std;
int wordCounter=0;
int pWordCounter=0;
string a[100];
bool yj();
bool bl(){
if(!a[pWordCounter].compare("i")){
pWordCounter+=1;
return true;
}else{
return false;
}
}
bool bds_prime(){
if(!a[pWordCounter].compare("+")){
pWordCounter+=1;
if(bl()){
if(bds_prime()){
return true;
}else{
return false;
}
}else{
return false;
}
}else if(!a[pWordCounter].compare("end")){
return true;
}else{
return true;
}
}
bool bds(){
if(bl()){
if(bds_prime()){
return true;
}else{
return false;
}
}else{
return false;
}
}
bool tjyj(){
if(!a[pWordCounter].compare("if")){
pWordCounter+=1;
if(bds()){
if(!a[pWordCounter].compare("then")){
pWordCounter+=1;
if(yj()){
return true;
}else{
return false;
}
}else{
return false;
}
}else{
return false;
}
}else{
return false;
}
}
bool fzyj(){
if(bl()){
if(!a[pWordCounter].compare(":")){
pWordCounter+=1;
if(!a[pWordCounter].compare("=")){
pWordCounter+=1;
if(bds()){
return true;
}else{
return false;
}
}else{
return false;
}
}else{
return false;
}
}else{
return false;
}
}
bool yj(){
if(fzyj()){
return true;
}else if(tjyj()){
return true;
}else{
return false;
}
}
bool cx(){
if(!a[pWordCounter].compare("begin")){
pWordCounter+=1;
if(yj()){
if(!a[pWordCounter].compare("end")){
return true;
}else{
return false;
}
}else{
return false;
}
}else{
return false;
}
}
int main(int argc, const char * argv[]) {
while(1){
cin>>a[wordCounter++];
if(!a[wordCounter-1].compare("end")){
break;
}
}
if(cx()){
cout<<"Success!"<<endl;
}else{
cout<<"Error!"<<endl;
}
return 0;
}
|
测试结果
测试用例如下:
1
2
3
4
5
| //begin i : = i + i end
//begin if i then i : = i + i end
//begin if i then if i then i : = i + i end
//begin end
//begin a : = i + j end
|
结果如下:
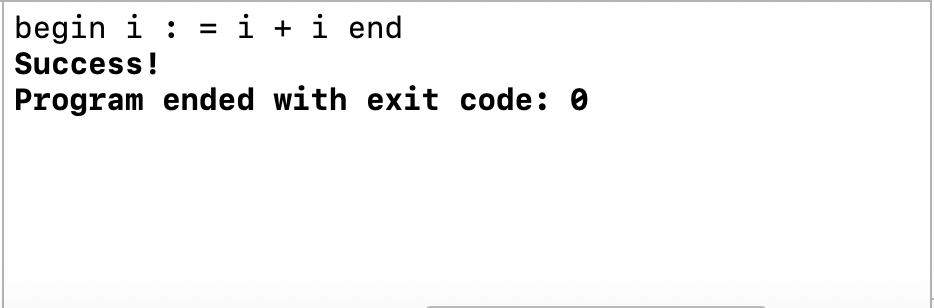


可证明该程序可实现要求功能。






















