Fy J
CS专业扫雷学深造学者互联网冲浪一级选手
FRIENDS
jhn

操作系统四：页面置换算法

05-17-2019 15:22:51 操作系统
Word count: 8.5k | Reading time: 34min

原创文章，转载、引用请注明出处！
代码、文章及图片挂载地址：https://github.com/MoyangSensei/OS

题目

页面置换算法

最佳置换算法、先进先出置换算法、最近最久未使用置换算法、改进型CLOCK置换算法、页面缓冲置换算法

符合局部访问特性的随机生成算法

（1）确定虚拟内存的尺寸N，工作集的起始位置p，工作集中包含的页数e，工作集移动率m（每处理m个页面访问则将起始位置p +1），以及一个范围在0和1之间的值t；

（2）生成m个取值范围在p和p + e间的随机数，并记录到页面访问序列串中；

（3）生成一个随机数r，0 ≤ r ≤ 1；

（4）如果r < t，则为p生成一个新值，否则p = (p + 1) mod N；

（5）如果想继续加大页面访问序列串的长度，请返回第2步，否则结束。

性能评测

（1）测试不同的页面访问序列及不同的虚拟内存尺寸，并从缺页率、算法开销等方面对各个算法进行比较。

（2）给出在给定页面访问序列的情况下，发生页面置换次数的平均值

解答

页面置换算法

在地址映射过程中，若在页面中发现所要访问的页面不在内存中，则产生缺页中断。当发生缺页中断时，如果操作系统内存中没有空闲页面，则操作系统必须在内存选择一个页面将其移出内存，以便为即将调入的页面让出空间。而用来选择淘汰哪一页的规则叫做页面置换算法。

前提及定义

由于在不同的操作系统和不同的情况下，页面置换算法的实现方式和效率是有一定出入的，因此先要对该过程的前提做规定和解释，以及对一些特定的变量作出说明。

前提

  • 对于给定的页面序列，程序或功能将严格按照这个顺序进行访问，不会出现提前访问、越界访问情况；

  • 对于给定的页面序列，每个页面的大小一定不会超过虚拟内存的大小；

  • 对于PBA算法，需要另外给定空闲物理块数量，该数量不可超过工作物理块数量；

  • 对于所有算法的页面填充过程，将新到来的页面填充到空白的工作物理块中，同样算作缺页。

定义

  • 对于各算法都通用的变量，定义如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    #define MAX 1024
    //页面序列总长度、工作集的起始位置p、物理块个数
    int pageNum=0,pageStart=0,blockNum=0;
    //物理块状态数组
    int **blockSta;
    //页面序列数组
    int *page;
    //页面序列指针
    int pPage;
    //缺页中断数组
    char *interrupt;
    //缺页数量
    int lakePage;
    //虚拟内存N
    int memory;
    //工作集中包含的页数e
    int everyWorkSet;
    //工作集移动率m
    int moveRate;

  • 对于最近最久未使用置换算法（LRU）来说，需要维护一个特定的栈，该栈的功能是：当前栈顶的页面就是最长时间没有被调用过的页面。
    该模拟栈以数组实现：

    1
    2
    3
    //自写栈的定义
        int stack[MAX];
        int top=-1;

  • 栈的功能以函数形式定义如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    //判断数组中是否已有x，若有返回其下标值，没有则返回-1
    int judge(int a[],int n,int x){
        int i;
        for(i=0;i<n;i++)
            if(x==a[i])
                return i;
        return -1;
    }
    //栈法插入(第一个元素出，后面元素前移，新元素从尾部入)
    void insert(int a[],int n,int x){
        int i;
        for(i=0;i<n-1;i++)
            a[i]=a[i+1];
        a[n-1]=x;
    }
    //移动下标为i的元素到尾部
    void move(int a[],int n,int i){
        int j;
        int m=a[i];
        for(j=i;j<n-1;j++)
            a[j]=a[j+1];
        a[n-1]=m;
    }

  • 对于改进型CLOCK算法来说，需要维护使用位、修改位以及生成随机的修改序列。
    使用位、修改位定义如下：

    1
    2
    3
    4
    5
    6
    //使用位
    bool *useBit;
    //修改位
    bool *modifiedBit;
    //修改页面序列
    bool *modifiedPage;

  • 函数getRandomModifiedPage用来生成随机的修改页面序列：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    void getRandomModifiedPage(){
        srand((unsigned)time(NULL));
        //设置修改页面数量占页面总数量的比重
        //此处默认为0.3
        double modifiedRate=0.3;
        int modifiedPageNum=ceil(pageNum*modifiedRate);
        int *a;
        a=(int*)malloc(sizeof(int)*modifiedPageNum);
        int flag=0,t=0;
        //随机编号为0到pageNum-1的页面序列编号中生成modifiedPageNum个修改页面
        for(;;){
            flag=0;
            if(t==modifiedPageNum){
                break;
            }
            int RandNum = (rand()%(pageNum-0))+0;
            for(int i = 0; i < t; i++){
                if(a[i] == RandNum)
                    flag = 1;
            }
            if(flag != 1){
                a[t] = RandNum;
                modifiedPage[a[t]]=true;
                t++;
            }
        }
    }

  • 对于页面缓冲置换算法（LRU）来说，需要维护空闲物理块。定义如下：

    1
    2
    3
    4
    //空闲物理块数量
    int freeBlock;
    //空闲物理块状态数组
    int **freeBlockSta;

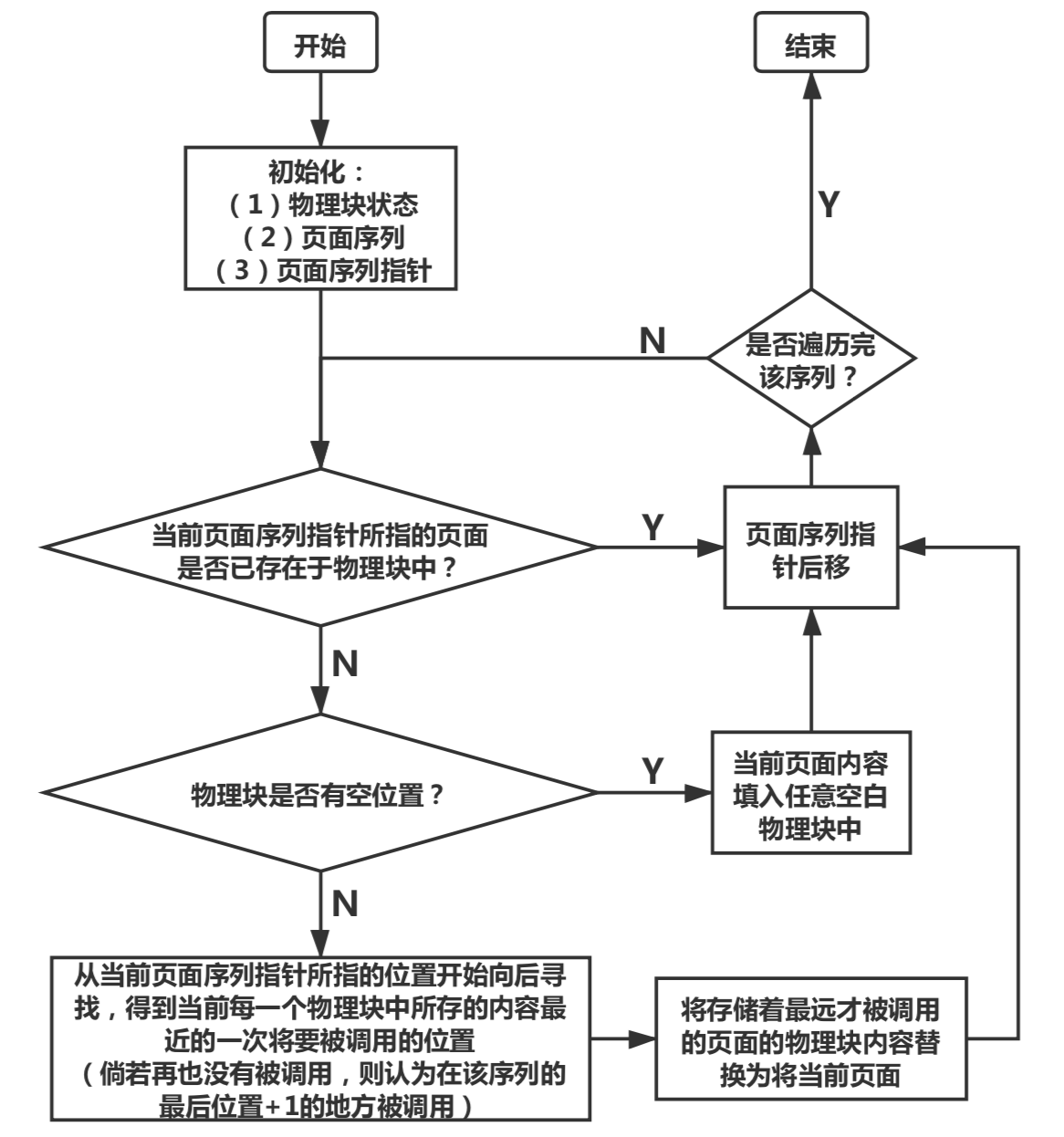
最佳置换算法（OPT）

概念

最佳置换算法（OPT）是一种理想情况下的页面置换算法，但实际上是不可能实现的。

该算法的基本思想是：发生缺页时，有些页面在内存中，其中有一页将很快被访问（也包含紧接着的下一条指令的那页），而其他页面则可能要到10、100或者1000条指令后才会被访问，每个页面都可以用在该页面首次被访问前所要执行的指令数进行标记。

最佳页面置换算法只是简单地规定：标记最大的页应该被置换。这个算法唯一的一个问题就是它无法实现。当缺页发生时，操作系统无法知道各个页面下一次是在什么时候被访问。对于我们的实验而言，由于我们给定了将要访问的页面的顺序序列，就相当于正确“预言”了接下来将要访问的页面，才能将这个算法实现出来。

虽然这个算法在实际情况不可能实现，但是最佳页面置换算法可以用于对可实现算法的性能进行衡量比较。

算法流程

最佳页面置换算法流程

代码及注释

函数**void OPT()**用来实现最佳置换算法的流程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
void OPT(){
    //缺页数量初始化
    lakePage=0;
    //页面序列指针初始化
    pPage=0;
    //缺页中断记录初始化
    for(int i=0;i<pageNum;i++){
        interrupt[i]='N';
    }
    //将物理块填充满
    fillFront();
    //使用位初始化（此处用作缺页数列的填充）
    for(int i=0;i<blockNum;i++){
        useBit[i]=false;
    }
    //将物理块填充过程中的缺页补全，替换块指针不动（填充完后又回到第一个位置）
    //从第1页到第pPage页共产生blockNum个缺页中断
    for(int i=0;i<pPage;i++){
        for(int j=0;j<blockNum;j++){
            if(page[i]==blockSta[j][pPage-1]){
                if(!useBit[j]){
                    useBit[j]=true;
                    interrupt[i]='Y';
                    lakePage+=1;
                }
                break;
            }
        }
    }
    //从能填充满物理块的那一个页面的下一个页面起开始遍历
    for(int i=pPage;i<pageNum;i++){
        //寻找所有的物理块内是否存储了当前所查找的页面i
        bool findPage = false;
        for(int j=0; j<blockNum; j++){
            if(page[i]==blockSta[j][i-1]){
                findPage=true;
                break;
            }
        }
        //将前一个页面所对应的物理块状态复制到当前页面所对应的物理块状态
        for(int j=0;j<blockNum;j++){
            blockSta[j][i]=blockSta[j][i-1];
        }
        //物理块内已存在相同页面
        if(findPage){
            //上一页面的物理块状态就是当前页面的物理块状态
            //上一页面的物理块状态已复制，直接进行下一页面即可
            continue;
        }
        //物理块内不存在相同页面
        else{
            //产生缺页
            lakePage+=1;
            interrupt[i]='Y';
            //nearPage：记录最近要被调用的位置
            int *nearPage;
            //ifFindNearPage：记录从该页面的下一个页面起到序列结束，是否有当前页面的调用
            bool *ifFindNearPage;
            nearPage=(int*)malloc(blockNum*sizeof(int));
            ifFindNearPage=(bool*)malloc(blockNum*sizeof(bool));
            //向着页面序列结束的方向寻找当前物理块每一个内容最近要被调用的位置
            for(int j=0;j<blockNum;j++){
                nearPage[j]=-1;
                ifFindNearPage[j]=false;
                for(int k=i+1;k<pageNum;k++){
                    if(blockSta[j][i]==page[k]){
                        nearPage[j]=k;
                        //找到调用：记录调用位置
                        ifFindNearPage[j]=true;
                        break;
                    }
                }
                //直到序列结束都未找到调用：调用位置设为序列长度+1
                if(!ifFindNearPage[j]){
                    nearPage[j]=pageNum+1;
                }
            }
            //找到最远调用的物理块
            int farPageNum=0,farPage=nearPage[0];
            for(int j=1;j<blockNum;j++){
                if(farPage<nearPage[j]){
                    farPage=nearPage[j];
                    farPageNum=j;
                }
            }
            //替换最远调用物理块中的内容为当前页面
            blockSta[farPageNum][i]=page[i];
        }
    }
}

物理块的填充

对于上述算法来说，在第8行调用了一个名为fillFront()的函数，该函数的功能是将物理块从全部空白填充至刚好所有物理块中都有不一样的内容。

实际上，这个过程是非常容易想到的，即一旦遇到新的页面后，将它填充到空白物理块中即可。但是这里需要注意的是：对于一个拥有n个模拟物理块的页面置换流程来说，如果前n个页面都是两两不相同的页面，那么该过程刚好可以把这n个不相同的页面全部填充进去，从第n+1个页面开始进行淘汰和替换动作。

但由于我们模拟的页面序列是有局部性的，即如果不指定工作集中包含的页数e远大于工作集移动率m，这种情况几乎是很少发生的。有可能出现这样的状况：

参数 过程
页面序列 1 2 2 3 …
物理块[1] 1 1 1 1 …
物理块[2] - 2 2 2 …
物理块[3] - - - 3 …

上面的例子告诉我们，如果前n个页面中出现了重复，那么将这n个模拟物理块从全部空白填充至全部非空白所需要的“步数”就不是n了。且不论是什么样的页面置换算法，只有在将空白物理块全部利用之后才会去考虑淘汰和替换的问题。因此，按照这个思路考虑，我们的所有页面置换算法分为两个步骤进行：

（1）先使用一个函数来帮我们将物理块从全部空白填充至刚好所有物理块中都有不一样的内容；

（2）只对剩余的页面序列考虑淘汰和替换问题。

函数**void fillFront()**用来实现物理块填充的流程。简言之，该函数的作用是避免在此过程中的重复元素多占用物理块。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void fillFront(){
    pPage=0;
    int a=0;
    int b[blockNum];
    for(int i=0;a<blockNum;i++){
        if(i==0){
            blockSta[0][0]=page[pPage];
            b[a]=page[pPage];
            a+=1;
        }else{
            for(int j=0;j<blockNum;j++){
                blockSta[j][pPage]=blockSta[j][pPage-1];
            }
            bool ifFindCommon=false;
            for(int j=0;j<a;j++){
                if(page[pPage]==b[j]){
                    ifFindCommon=true;
                    break;
                }
            }
            if(!ifFindCommon){
                blockSta[a][pPage]=page[pPage];
                b[a]=page[pPage];
                a+=1;
            }
        }
        pPage+=1;
    }
}

该函数适用于FIFO、OPT、改进型CLOCK以及PBA，之后不再赘述。

该函数不适用于LRU：虽然是同样的填充方法，但是LRU要从头开始维护一个特殊的栈，代表物理块中的页面是否在最近被调用过。重复页面会使得该页面在特殊的栈的“位置”变得“靠前”，而其他算法并不考虑已检索的重复页面对于整个算法流程的影响（OPT考虑的是未检索过的重复页面）。

此函数仅仅是为了方便代码的编写以及理解整个流程，模拟算法可用之。在实际情况下一定是在分配的物理块区域内按照顺序进行检索的。

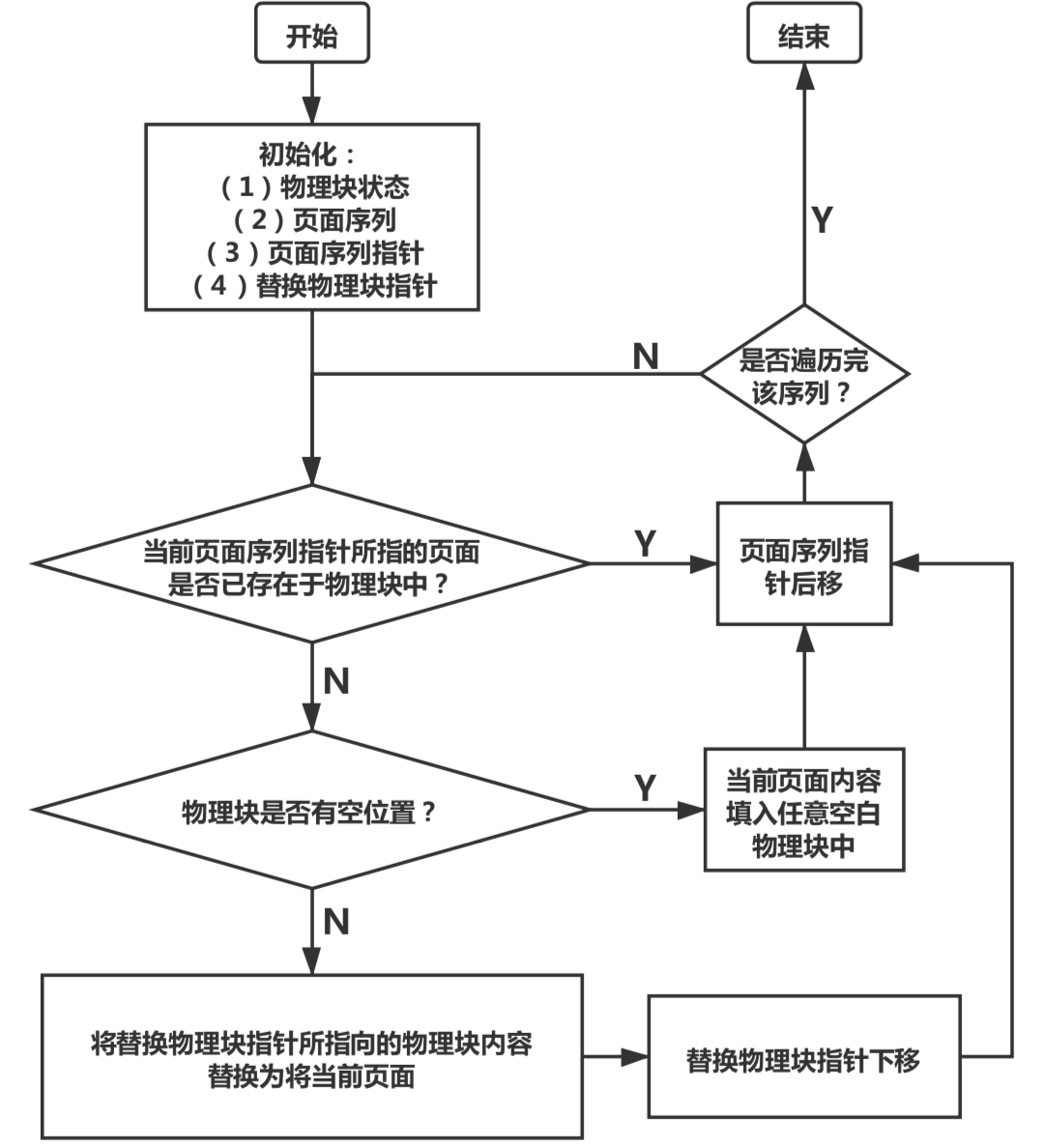
先进先出置换算法（FIFO）

概念

先进先出置换算法是实现最为简单的置换算法，只需把调入内存的页面根据先后次序链接成队列，设置一个指针总指向最早的页面。

其基本思想是：优先淘汰最早进入内存的页面，亦即在内存中驻留时间最久的页面。

但FIFO算法与进程实际运行时的规律不适应，因为在进程中，有的页面经常被访问。且FIFO算法还会产生当所分配的物理块数增大而页故障数不减反增的异常现象，这是由Belady于1969年发现，故称为Belady异常。

只有FIFO算法可能出现Belady异常，而LRU和OPT算法永远不会出现Belady异常。

算法流程

先进先出置换算法流程

代码及注释

函数**void FIFO()**用来实现最佳置换算法的流程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
void FIFO(){
    //缺页数量初始化
    lakePage=0;
    //页面序列指针初始化
    pPage=0;
    //缺页中断记录初始化
    for(int i=0;i<pageNum;i++){
        interrupt[i]='N';
    }
    //将物理块填充满
    fillFront();
    //使用位初始化（此处用作缺页数列的填充）
    for(int i=0;i<blockNum;i++){
        useBit[i]=false;
    }
    //将物理块填充过程中的缺页补全
    //从第1页到第pPage页共产生blockNum个缺页中断
    for(int i=0;i<pPage;i++){
        for(int j=0;j<blockNum;j++){
            if(page[i]==blockSta[j][pPage-1]){
                if(!useBit[j]){
                    useBit[j]=true;
                    interrupt[i]='Y';
                    lakePage+=1;
                }
                break;
            }
        }
    }
    //设置替换块指针
    int pReplaceBlock=0;
    //从能填充满物理块的那一个页面的下一个页面起开始遍历
    for(int i=pPage;i<pageNum;i++){
        //寻找所有的物理块内是否存储了当前所查找的页面i
        bool findPage = false;
        for(int j=0; j<blockNum; j++){
            if(page[i]==blockSta[j][i-1]){
                findPage=true;
                break;
            }
        }
        //将前一个页面所对应的物理块状态复制到当前页面所对应的物理块状态
        for(int j=0;j<blockNum;j++){
            blockSta[j][i]=blockSta[j][i-1];
        }
        //物理块内已存在相同页面
        if(findPage){
            //上一页面的物理块状态就是当前页面的物理块状态
            //上一页面的物理块状态已复制，直接进行下一页面即可
            continue;
        }
        //物理块内不存在相同页面
        else{
            //产生缺页
            lakePage+=1;
            interrupt[i]='Y';
            //将替换指针所指向的物理块进行替换
            blockSta[pReplaceBlock][i]=page[i];
            //将替换指针后移
            pReplaceBlock=(pReplaceBlock+1)%blockNum;
        }
    }
}

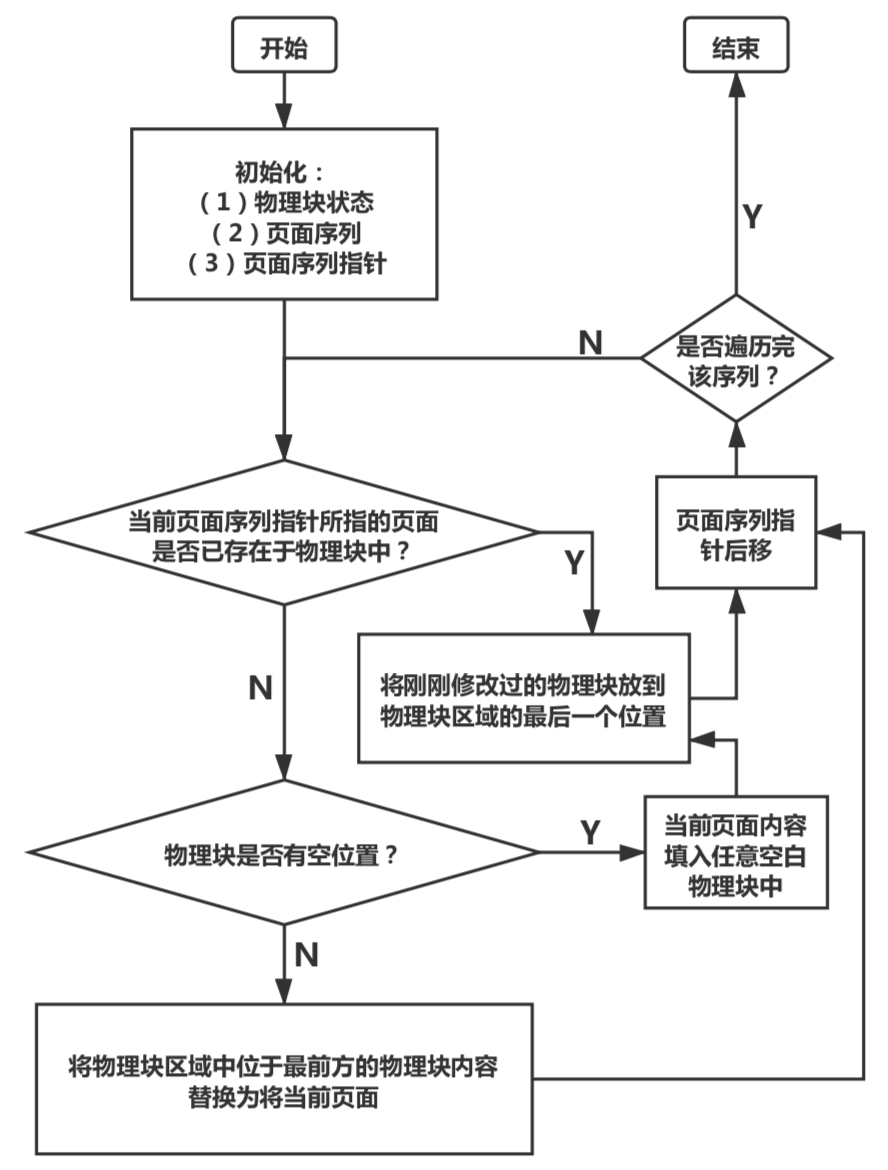
最近最久未使用置换算法（LRU）

概念

在之前的FIFO算法中，依据的是各个页面调入内存的时间，这并不能反映页面的真实使用情况。

而最近最久未使用置换算法（Latest Recently Used）是根据页面调入内存之后的使用情况。由于无法预测页面未来的情况，所以只能利用“最近的过去”来作为预测未来的方法，LRU选择的是最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段，用来记录一个页面从上次被访问以来所经历的时间t，当需要淘汰一个页面的时候，选择现有页面中t的值最大的页面进行淘汰。

LRU是一种优秀的页面置换算法，但是需要硬件的支持，为了了解一个进程在内存中各个页面各有多少时间未被进程访问，以及如何快速地知道哪一个页面是最近最久未使用的页面，需要寄存器或栈来支持。

（1）寄存器：为了记录某进程在内存中各页的使用情况，需要为每个在内存中的页面设置一个移位寄存器，可表示为：R=R(n-1)R(n-2)…R2R1R0,当进程访问某物理块时，要将相应寄存器的R(n-1)位置成1。此时，定时信号将每隔一定时间（例如100ms）将寄存器右移一位。如果我们把n位寄存器的数看做是一个整数，那么具有最小数值的寄存器所对应的页面，就是最近最久未使用的页面。当发生缺页时，首先将它置换出去。

（2）栈：可以利用一种特殊的栈来保存当前使用的各个页面的页面号，每当进程访问某页面的时候，便将该页面的页面号从栈中移除，将它压入栈顶。因此，栈顶始终是最新被访问页面的编号，栈底则是最近最久未访问页面的页面号，当需要置换页面的时候，将栈底对应的页面置换出来。

算法流程

最近最久未使用置换算法流程

代码及注释

函数**void LRU()**用来实现最佳置换算法的流程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
void LRU(){
    //缺页数量初始化
    lakePage=0;
    //页面序列指针初始化
    pPage=0;
    //缺页中断记录初始化
    for(int i=0;i<pageNum;i++){
        interrupt[i]='N';
    }
    //自写栈的定义
    int stack[MAX];
    int top=-1;
    //初始化自写栈
    for(int i=0;i<blockNum;i++){
        stack[i]=-1;
    }
    //从页面序列的第一个开始遍历
    for(int i=0;i<pageNum;i++){
        //读数后top自动+1
        top++;
        //栈中无元素：直接插入元素
        if(top==0){
            stack[top]=page[i];
            lakePage+=1;
            interrupt[i]='Y';
        }
        //栈中元素个数小于物理块个数：不重复则直接插入、重复则更新元素在栈中位置
        else if(top<blockNum){
            //栈中不存在待插入元素：新元素从尾部插入
            if(judge(stack,blockNum,page[i])==-1){
                stack[top]=page[i];
                lakePage+=1;
                interrupt[i]='Y';
            }
            //栈中存在待插入元素：重复元素的位置置后，表示最近使用过
            else{
                move(stack,top,judge(stack,blockNum,page[i]));
                top--;
            }
        }
        //栈中元素个数大于物理块个数：重复则更新元素在栈中位置、不重复就淘汰并替换元素
        else{
            //栈中不存在待插入元素：新元素栈法插入（淘汰替换旧元素）
            //栈法插入：第一个元素出，后面元素前移，新元素从尾部入
            //产生缺页
            if(judge(stack,blockNum,page[i])==-1){
                insert(stack,blockNum,page[i]);
                lakePage+=1;
                interrupt[i]='Y';
                top--;
            }
            //栈中存在待插入元素：重复元素的位置置后，表示最近使用过
            else{
                move(stack,blockNum,judge(stack,blockNum,page[i]));
                top--;
            }
        }
        //更新物理块的变化情况
        for(int j=0;j<blockNum;j++){
            if(stack[j]!=-1){
                blockSta[j][i]=stack[j];
            }
        }
    }
}

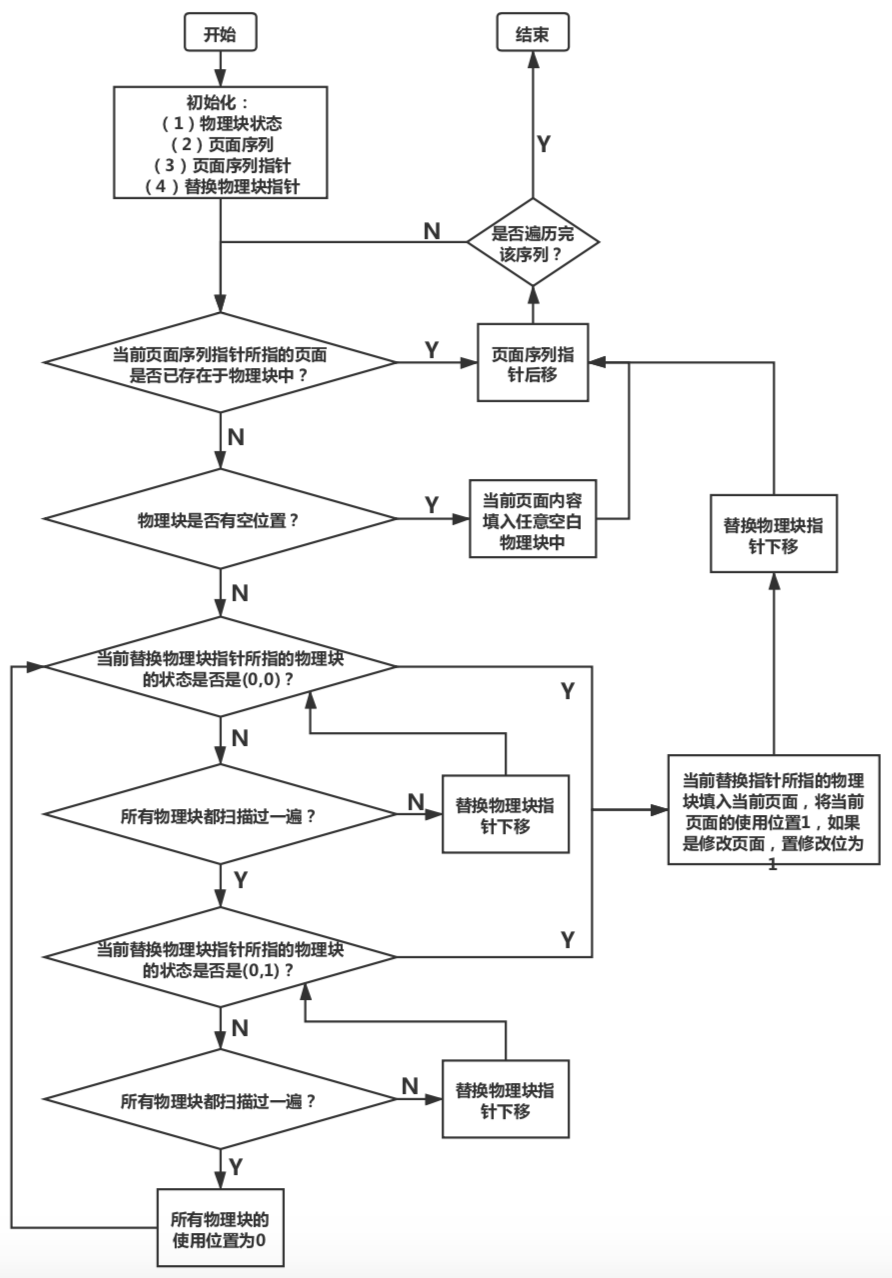
改进型Clock置换算法

概念

简单的CLOCK算法是给每一帧关联一个附加位，称为使用位。当某一页首次装入主存时，该帧的使用位设置为1；当该页随后再被访问到时，它的使用位也被置为1。对于页替换算法，用于替换的候选帧集合看做一个循环缓冲区，并且有一个指针与之相关联。当某一页被替换时，该指针被设置成指向缓冲区中的下一帧。当需要替换一页时，操作系统扫描缓冲区，以查找使用位被置为0的一帧。每当遇到一个使用位为1的帧时，操作系统就将该位重新置为0；如果在这个过程开始时，缓冲区中所有帧的使用位均为0，则选择遇到的第一个帧替换；如果所有帧的使用位均为1,则指针在缓冲区中完整地循环一周，把所有使用位都置为0，并且停留在最初的位置上，替换该帧中的页。由于该算法循环地检查各页面的情况，故称为CLOCK算法，又称为最近未用(Not Recently Used, NRU)算法。

CLOCK算法的性能比较接近LRU，而通过增加使用的位数目，可以使得CLOCK算法更加高效。在使用位的基础上再增加一个修改位，则得到改进型的CLOCK置换算法。这样，每一帧都处于以下四种情况之一：

  • 最近未被访问，也未被修改(u=0, m=0)。

  • 最近被访问，但未被修改(u=1, m=0)。

  • 最近未被访问，但被修改(u=0, m=1)。

  • 最近被访问，被修改(u=1, m=1)。

在改进型CLOCK算法中，系统总是倾向于替换最近未被访问且未被修改的页面，倘若不存在这样的页面，那么系统就回去寻找最近被访问但为不修改的页面。倘若无法在为修改页面中找到符合上述两条条件的页面，那么系统就会将所有物理块均视作未访问，再去进行上述查询过程。如此这般，一定可以找到一个符合条件的页面，来进行当前页面的淘汰和替换。

算法流程

改进型CLOCK置换算法流程

代码及注释

函数**void CLOCK_better()**用来实现最佳置换算法的流程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
void CLOCK_better(){
    //缺页数量初始化
    lakePage=0;
    //页面序列指针初始化
    pPage=0;
    //缺页中断记录初始化
    for(int i=0;i<pageNum;i++){
        interrupt[i]='N';
    }
    //使用位初始化（此处用作缺页数列的填充）
    for(int i=0;i<blockNum;i++){
        useBit[i]=false;
    }
    //随机生成修改页序列
    getRandomModifiedPage();
    //将物理块填充满
    fillFront();
    //设置替换块指针
    int pReplaceBlock=0;
    //将物理块填充过程中的使用位和修改位、缺页补全，替换块指针不动（填充完后又回到第一个位置）
    //从第1页到第pPage页共产生blockNum个缺页中断
    //所有的useBit全部为1
    for(int i=0;i<pPage;i++){
        for(int j=0;j<blockNum;j++){
            if(page[i]==blockSta[j][pPage-1]){
                if(!useBit[j]){
                    useBit[j]=true;
                    interrupt[i]='Y';
                    lakePage+=1;
                }
                if(modifiedPage[i]){
                    modifiedBit[j]=true;
                }
                break;
            }
        }
    }
    //从能填充满物理块的那一个页面的下一个页面起开始遍历
    for(int i=pPage;i<pageNum;i++){
        //寻找所有的物理块内是否存储了当前所查找的页面i
        bool findPage = false;
        for(int j=0; j<blockNum; j++){
            if(page[i]==blockSta[j][i-1]){
                findPage=true;
                break;
            }
        }
        //将前一个页面所对应的物理块状态复制到当前页面所对应的物理块状态
        for(int j=0;j<blockNum;j++){
            blockSta[j][i]=blockSta[j][i-1];
        }
        //物理块内已存在相同页面
        if(findPage){
            //上一页面的物理块状态就是当前页面的物理块状态
            //上一页面的物理块状态已复制，直接进行下一页面即可
            continue;
        }
        //物理块内不存在相同页面
        else{
            //产生缺页
            lakePage+=1;
            interrupt[i]='Y';
            bool ifFindReplaceBlock=false;
            ////////////////////////////////////////////////////////////////////
            //第一次寻找：find(0,0)
            for(int j=0;j<blockNum;j++){
                if(!useBit[pReplaceBlock]&&!modifiedPage[pReplaceBlock]){
                    ifFindReplaceBlock=true;
                    break;
                }else{
                    pReplaceBlock=(pReplaceBlock+1)%blockNum;
                }
            }
            if(ifFindReplaceBlock){
                blockSta[pReplaceBlock][i]=page[i];
                if(modifiedPage[i]){
                    modifiedBit[pReplaceBlock]=true;
                }
                pReplaceBlock=(pReplaceBlock+1)%blockNum;
                continue;
            }
            ////////////////////////////////////////////////////////////////////
            //第二次寻找：find(0,1)
            for(int j=0;j<blockNum;j++){
                if(!useBit[pReplaceBlock]&&modifiedPage[pReplaceBlock]){
                    ifFindReplaceBlock=true;
                    break;
                }else{
                    pReplaceBlock=(pReplaceBlock+1)%blockNum;
                }
            }
            if(ifFindReplaceBlock){
                blockSta[pReplaceBlock][i]=page[i];
                if(modifiedPage[i]){
                    modifiedBit[pReplaceBlock]=true;
                }
                pReplaceBlock=(pReplaceBlock+1)%blockNum;
                continue;
            }
            ////////////////////////////////////////////////////////////////////
            //将集合中所有页面的使用位设置成0
            for(int j=0;j<blockNum;j++){
                useBit[j]=false;
            }
            ////////////////////////////////////////////////////////////////////
            //第三次寻找（使用位已修改）：find(0,0)
            for(int j=0;j<blockNum;j++){
                if(!useBit[pReplaceBlock]&&!modifiedPage[pReplaceBlock]){
                    ifFindReplaceBlock=true;
                    break;
                }else{
                    pReplaceBlock=(pReplaceBlock+1)%blockNum;
                }
            }
            if(ifFindReplaceBlock){
                blockSta[pReplaceBlock][i]=page[i];
                if(modifiedPage[i]){
                    modifiedBit[pReplaceBlock]=true;
                }
                useBit[pReplaceBlock]=true;
                pReplaceBlock=(pReplaceBlock+1)%blockNum;
                continue;
            }
            ////////////////////////////////////////////////////////////////////
            //第四次寻找（使用位已修改）：find(0,1)
            //如果进行到此处，一定可以找到结果，否则证明代码逻辑出现错误
            for(int j=0;j<blockNum;j++){
                if(!useBit[pReplaceBlock]&&modifiedPage[pReplaceBlock]){
                    ifFindReplaceBlock=true;
                    break;
                }else{
                    pReplaceBlock=(pReplaceBlock+1)%blockNum;
                }
            }
            if(ifFindReplaceBlock){
                blockSta[pReplaceBlock][i]=page[i];
                if(modifiedPage[i]){
                    modifiedBit[pReplaceBlock]=true;
                }
                useBit[pReplaceBlock]=true;
                pReplaceBlock=(pReplaceBlock+1)%blockNum;
                continue;
            }
        }
    }
}

页面缓冲算法（PBA）

概念

页面缓冲算法是目前Linux系统较为常见的一种页面置换算法。

当需要置换页面时，采用FIFO从所有以分配页面中选择最先进入的页面淘汰。该算法规定将一个被淘汰的页放入两个链表中的一个，即如果页面未被修改，就将它直接放入空闲链表中；否则，便放入已经修改页面的链表中的一个。须注意的是，这时页面在内存中并不做物理上的移动，而只是将页表中的表项移到上述两个链表之一中。

算法流程

页面缓冲算法流程

代码及注释

函数**void PBA()**用来实现最佳置换算法的流程。

该函数实现的PBA算法不是标准概念的实现，区别在于没有模拟修改页面物理块和对空闲物理块的数量进行动态分配，只是模拟了固定数量的空闲物理块的情况。

按照这样的思想去实现，可以推测，这样进行的流程结果，与FIFO是完全一致的（工作物理块的变化情况）。如果在把空闲物理块调用至工作物理块的步骤也算作缺页的前提下（这一点非常重要），连缺页率的计算结果也会和同情况下的FIFO一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
void PBA(){
    //缺页数量初始化
    lakePage=0;
    //页面序列指针初始化
    pPage=0;
    //缺页中断记录初始化
    for(int i=0;i<pageNum;i++){
        interrupt[i]='N';
    }
    //将物理块填充满
    fillFront();
    //设置替换块指针：此处的更替指针的原理与FIFO是相同的
    int pReplaceBlock=0;
    //使用位初始化（此处用作缺页数列的填充）
    for(int i=0;i<blockNum;i++){
        useBit[i]=false;
    }
    //将物理块填充过程中的缺页补全，替换块指针不动（填充完后又回到第一个位置）
    //从第1页到第pPage页共产生blockNum个缺页中断
    for(int i=0;i<pPage;i++){
        for(int j=0;j<blockNum;j++){
            if(page[i]==blockSta[j][pPage-1]){
                if(!useBit[j]){
                    useBit[j]=true;
                    interrupt[i]='Y';
                    lakePage+=1;
                }
                break;
            }
        }
    }
    //从能填充满物理块的那一个页面的下一个页面起开始遍历
    for(int i=pPage;i<pageNum;i++){
        //
        for(int j=0;j<freeBlock;j++){
            freeBlockSta[j][i]=freeBlockSta[j][i-1];
        }
        //寻找所有的物理块内是否存储了当前所查找的页面i
        bool findPage = false;
        for(int j=0; j<blockNum; j++){
            if(page[i]==blockSta[j][i-1]){
                findPage=true;
                break;
            }
        }
        //将前一个页面所对应的物理块状态复制到当前页面所对应的物理块状态
        for(int j=0;j<blockNum;j++){
            blockSta[j][i]=blockSta[j][i-1];
        }
        //物理块内已存在相同页面
        if(findPage){
            //上一页面的物理块状态就是当前页面的物理块状态
            //上一页面的物理块状态已复制，直接进行下一页面即可
            continue;
        }
        //物理块内不存在相同页面
        else{
            //是否在缓冲物理块内
            int inFreeBLockLocation=-1;
            for(int j=0;j<freeBlock;j++){
                if(page[i]==freeBlockSta[j][i]){
                    inFreeBLockLocation=j;
                    break;
                }
            }
            //在缓冲物理块内
            if(inFreeBLockLocation!=-1){
                //产生缺页
                lakePage+=1;
                interrupt[i]='Y';
                //将两块的内容交换
                int temp=blockSta[pReplaceBlock][i];
                blockSta[pReplaceBlock][i]=freeBlockSta[inFreeBLockLocation][i];
                freeBlockSta[inFreeBLockLocation][i]=temp;
                //将替换指针后移
                pReplaceBlock=(pReplaceBlock+1)%blockNum;
                //将这一块的内容放到最后
                for(int j=inFreeBLockLocation;j<freeBlock-1;j++){
                    freeBlockSta[j][i]=freeBlockSta[j+1][i];
                }
                freeBlockSta[freeBlock-1][i]=temp;
            }
            else{
                int spaceFreeBlock=-1;
                for(int j=0;j<freeBlock;j++){
                    if(freeBlockSta[j][i]==0){
                        spaceFreeBlock=j;
                        break;
                    }
                }
                //有空白的缓冲物理块：
                //当前物理块填入空白物理块
                //当前页面填入当前物理块
                if(spaceFreeBlock!=-1){
                    //产生缺页
                    lakePage+=1;
                    interrupt[i]='Y';
                    //将替换指针所指向的物理块进行替换
                    freeBlockSta[spaceFreeBlock][i]=blockSta[pReplaceBlock][i];
                    blockSta[pReplaceBlock][i]=page[i];
                    //将替换指针后移
                    pReplaceBlock=(pReplaceBlock+1)%blockNum;
                }
                //不存在空白的缓冲物理块
                //将空闲物理块的最后一个位置的内容替换成当前的页面，缺页操作同上
                else{
                    //产生缺页
                    lakePage+=1;
                    interrupt[i]='Y';
                    //temp保留当前物理块内容
                    //当前工作物理块填入当前页面作为新内容
                    int temp=blockSta[pReplaceBlock][i];
                    blockSta[pReplaceBlock][i]=page[i];
                    //抛弃空闲物理块第一块的内容，temp放入最后一块的内容
                    for(int j=0;j<freeBlock-1;j++){
                        freeBlockSta[j][i]=freeBlockSta[j+1][i];
                    }
                    freeBlockSta[freeBlock-1][i]=temp;
                    //将替换指针后移
                    pReplaceBlock=(pReplaceBlock+1)%blockNum;
                }
            }
        }
    }
}

页面序列随机算法

显而易见的是，用来测试上述页面置换算法的页面序列不可以用全随机的方式生成。不加限制的随机序列必然不符合局部性原理。如果页面序列不符合局部性，势必会使得缺页率大大增加。

实现题目中所给的页面序列随机算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//符合局部访问特性的随机生成算法
void getRandomPage(){
    srand((unsigned)time(NULL));
    double t=rand()%10/10.0;
    for(int i=0;i<(int)(pageNum/moveRate);i++){
        for(int j=i*moveRate;j<(i+1)*moveRate;j++){
            page[j]=(pageStart+rand()%everyWorkSet)%memory;
        }
        double r=rand()%10/10.0;
        if(r<t){
            pageStart=rand()%memory;
        }else{
            pageStart=(pageStart+1)%memory;
        }
    }
    //序列的最后几个内容的长度不足以构成工作集移动的一步，单另填充，规则不变
    for(int i=(int)(pageNum/moveRate)*moveRate;i<pageNum;i++){
        page[i]=(pageStart+rand()%everyWorkSet)%memory;
    }
    cout<<"生成的随机序列为: ";
    for(int i=0;i<pageNum;i++){
        cout<<page[i]<<" ";
    }
    cout<<endl<<endl;
}

运行结果及对比分析

输入

输入内容分为两部分，第一部分要输入页面序列长度、页面起始位置、物理块数、每个工作集包含的页面数、工作集移动率，共五个参数；第二部分针对PBA算法输入缓冲物理块数量，限制是该数量需要小于工作物理块数。

1
2
3
4
5
6
7
8
9
10
11
12
//键入信息
    cout<<"输入页面序列长度、页面起始位置、物理块数、每个工作集包含的页面数、工作集移动率:";
    cin>>pageNum>>pageStart>>blockNum>>everyWorkSet>>moveRate;
    cout<<"PBA算法中的缓冲物理块数量(需小于工作物理块数):";
    while(1){
        cin>>freeBlock;
        if(freeBlock<blockNum){
            break;
        }else{
            cout<<"缓冲物理块数量有误，请重新输入:";
        }
    }

在接下来的测试中，输入固定如下：

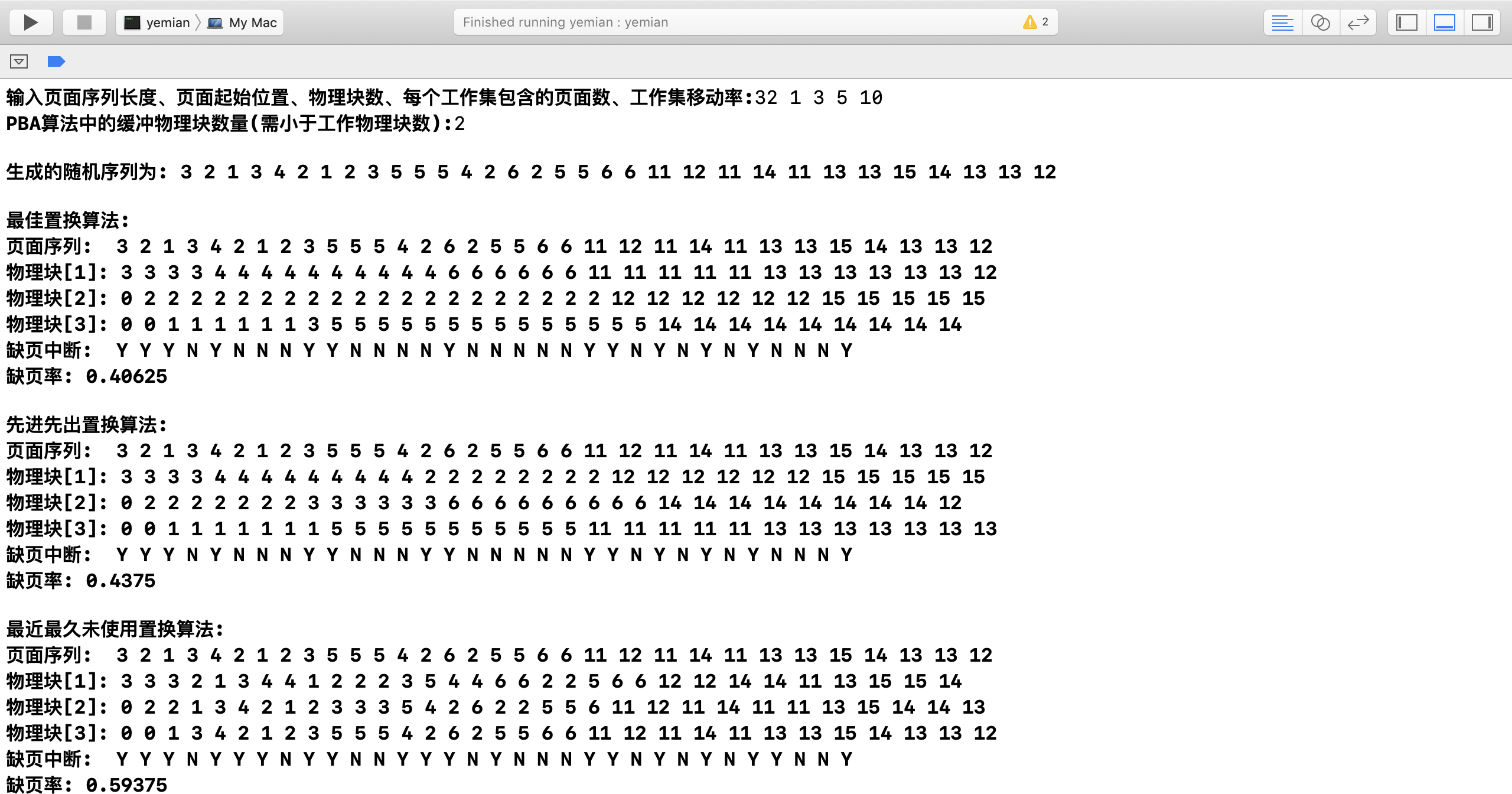
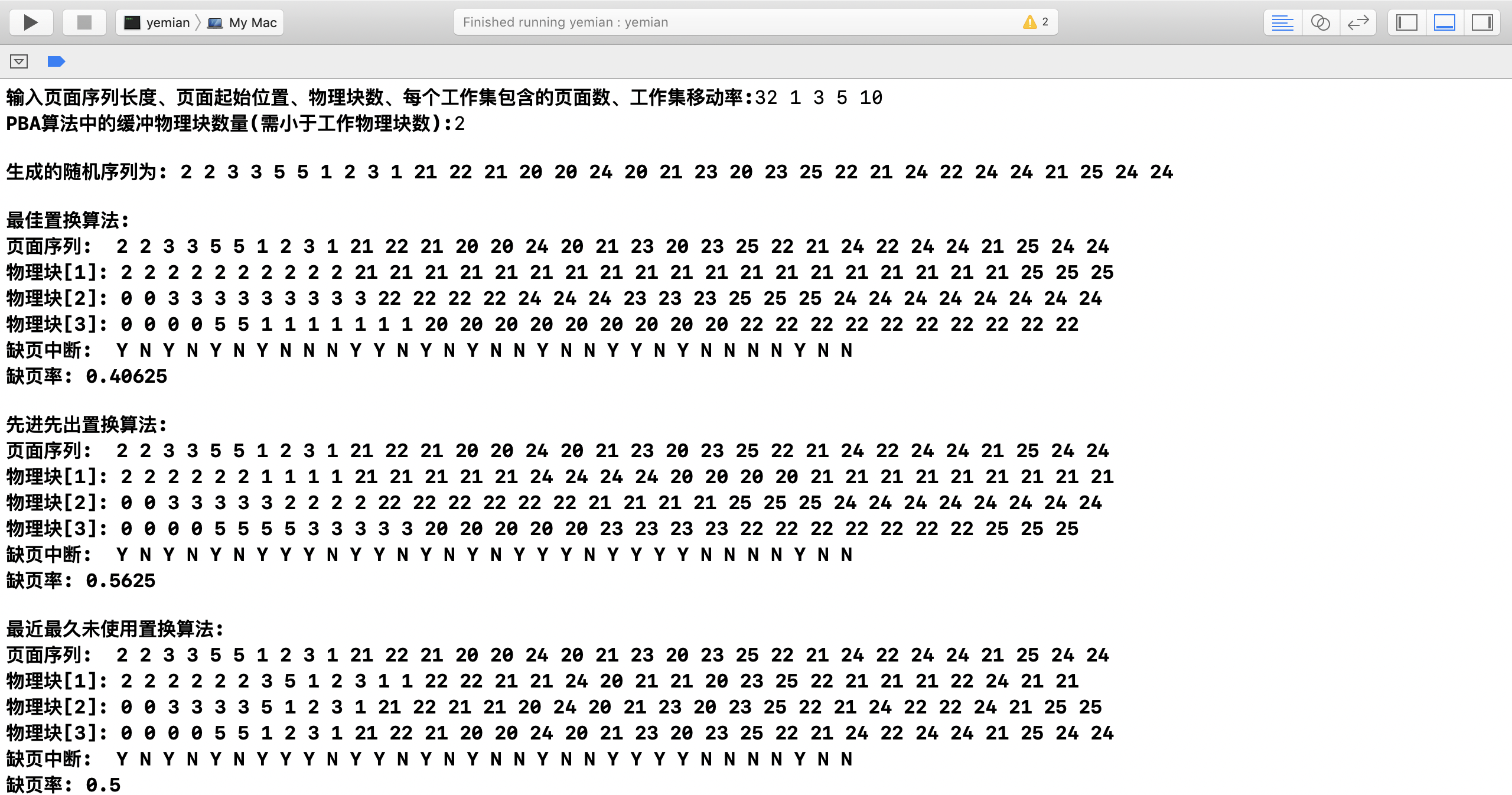
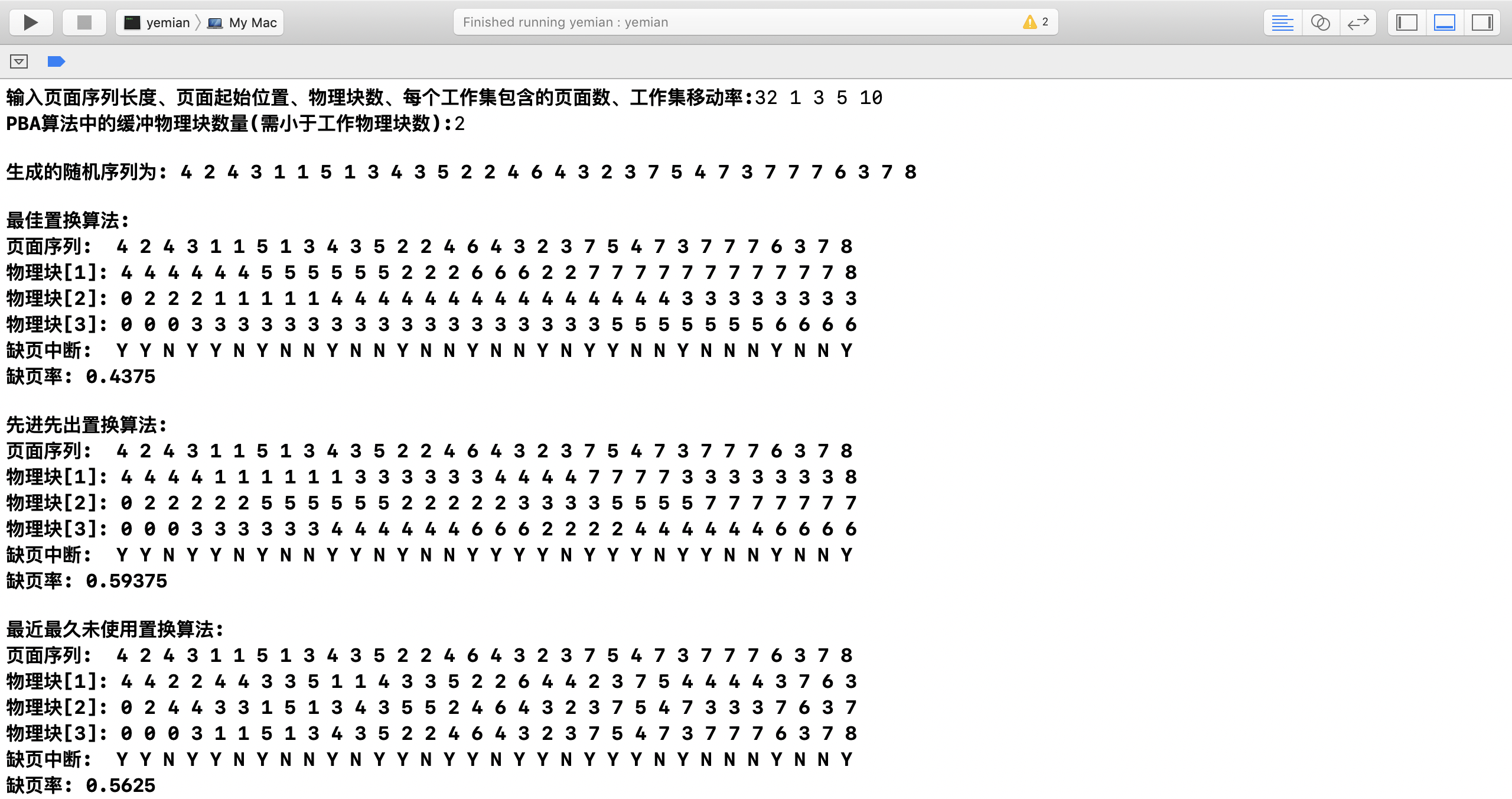
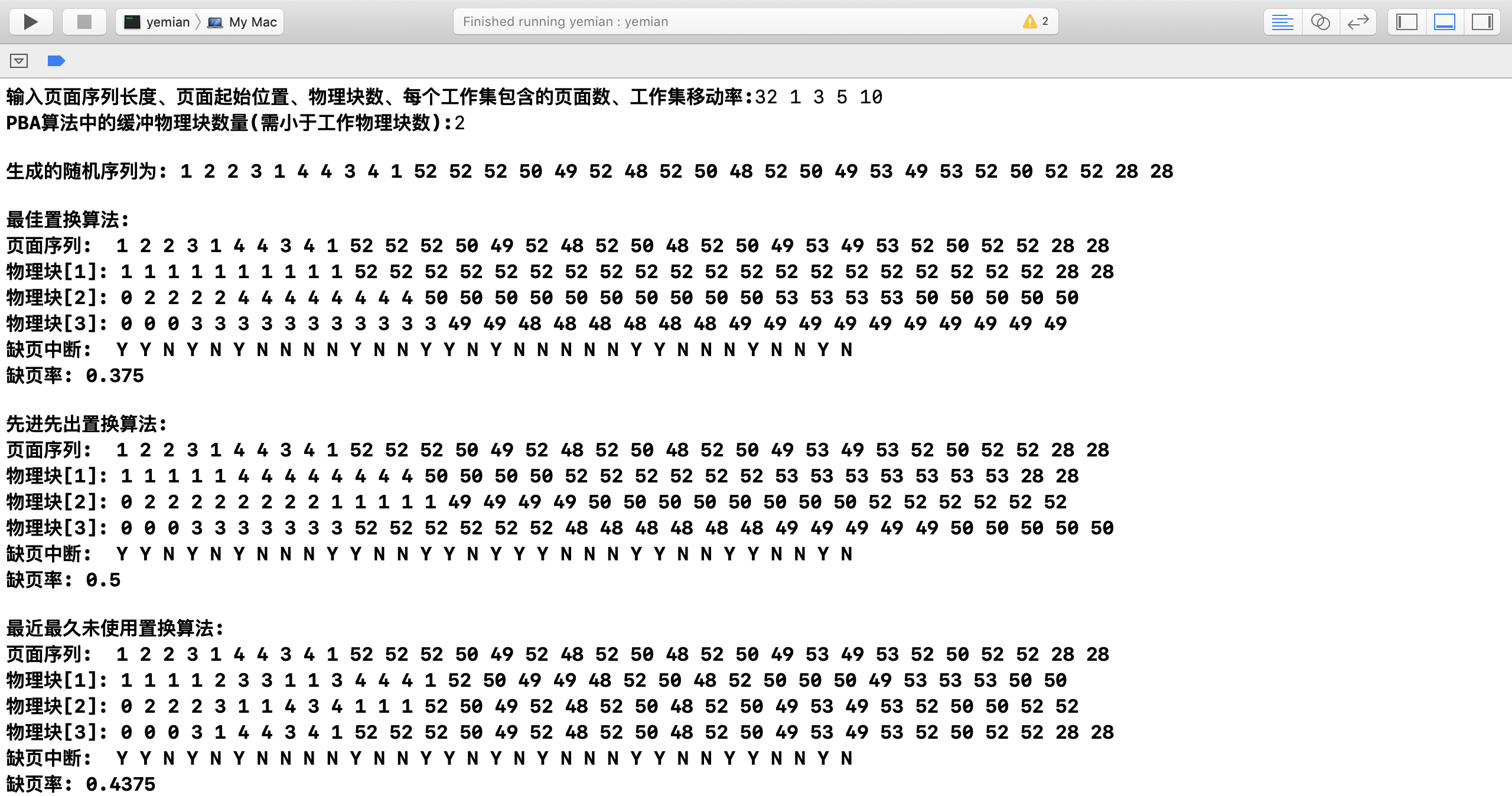
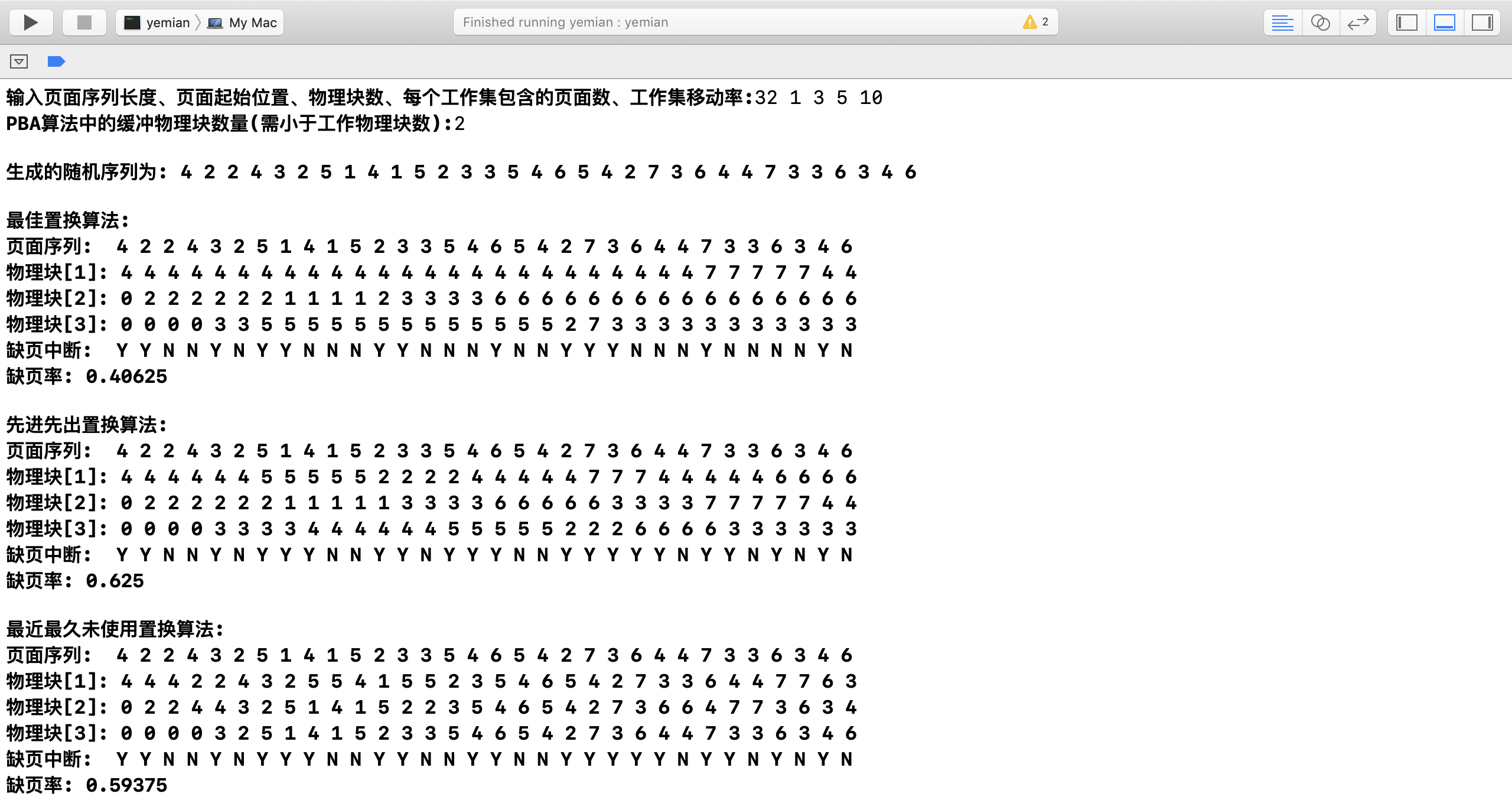
输入页面序列长度、页面起始位置、物理块数、每个工作集包含的页面数、工作集移动率:32 1 3 5 10
PBA算法中的缓冲物理块数量(需小于工作物理块数):2

运行结果

使用上面的输入，对于不同的随机序列，运行结果如下：

  • 第一次运行：

  • 第二次运行：

  • 第三次运行：

  • 第四次运行：

  • 第五次运行：

对比分析

  • 统计上述测试的缺页率：
算法 第一次运行 第二次运行 第三次运行 第四次运行 第五次运行
OPT 0.40625 0.40625 0.4375 0.375 0.40625
FIFO 0.4375 0.5625 0.59375 0.5 0.625
LRU 0.59375 0.5 0.5625 0.4375 0.59375
改进型CLOCK算法 0.71875 0.78125 0.71875 0.6875 0.65625
PBA 0.4375 0.5625 0.59375 0.5 0.625
  • 针对不同的算法，5次运行的缺页率均值如下：
OPT FIFO LRU 改进型CLOCK算法 PBA
0.40625 0.54375 0.5375 0.712 0.54375

首先，OPT的缺页率是所有算法中最低的，这同样符合该算法的定义和其命名“最佳”。

LRU算法的性能接近于OPT。但是从实现角度来说，其实现比较困难，且开销大：需要额外维护物理块中页面的调用顺序。

FIFO算法实现简单，但其机制决定了它的实际性能应该是最差的。PBA算法的缺页率和FIFO相同，这是由于模拟度不够且做了一些假设前提而导致的。它们的区别并不体现在缺页率上。

那么PBA和FIFO的区别何在？在于PBA将缺页内容放在缓冲块（空闲物理块）里，而不存入内存里，不需要去内存调用对应的块，从系统资源的角度来说，节省了系统开销。这一点在我们的模拟中是无法体现的。

所以操作系统的设计者尝试了很多算法，试图用比较小的开销接近LRU的性能，这类算法都是CLOCK算法的变体。但在上述测试中，改进型CLOCK算法的性能是最差的。由于该算法引入了修改页序列，所以导致了这一情况。可以推测，如果页面序列里没有修改页，即这些算法的流程是完全一致的，那么改进型CLOCK算法的性能会接近LRU，而FIFO的性能会变成最差。

参考链接

百度百科-页面置换算法：https://baike.baidu.com/item/页面置换算法/7626091?fr=aladdin

百度百科-最佳页面置换算法：https://baike.baidu.com/item/最佳页面置换算法/7626051?fr=aladdin

百度百科-先进先出页面置换算法：https://baike.baidu.com/item/先进先出页面置换算法/3286551

百度百科-局部性原理：https://baike.baidu.com/item/局部性原理/3334556?fr=aladdin

操作系统页面置换算法(opt,lru,fifo,clock)实现：https://hjzgg.github.io/resume/

< PreviousPost
编译原理：LL(1)语法分析NextPost >
编译原理：递归下降分析
CATALOG
  1. 1. 题目
    1. 1.1. 页面置换算法
    2. 1.2. 符合局部访问特性的随机生成算法
    3. 1.3. 性能评测
  2. 2. 解答
    1. 2.1. 页面置换算法
    2. 2.2. 前提及定义
      1. 2.2.1. 前提
      2. 2.2.2. 定义
    3. 2.3. 最佳置换算法（OPT）
      1. 2.3.1. 概念
      2. 2.3.2. 算法流程
      3. 2.3.3. 代码及注释
    4. 2.4. 物理块的填充
    5. 2.5. 先进先出置换算法（FIFO）
      1. 2.5.1. 概念
      2. 2.5.2. 算法流程
      3. 2.5.3. 代码及注释
    6. 2.6. 最近最久未使用置换算法（LRU）
      1. 2.6.1. 概念
      2. 2.6.2. 算法流程
      3. 2.6.3. 代码及注释
    7. 2.7. 改进型Clock置换算法
      1. 2.7.1. 概念
      2. 2.7.2. 算法流程
      3. 2.7.3. 代码及注释
    8. 2.8. 页面缓冲算法（PBA）
      1. 2.8.1. 概念
      2. 2.8.2. 算法流程
      3. 2.8.3. 代码及注释
    9. 2.9. 页面序列随机算法
    10. 2.10. 运行结果及对比分析
      1. 2.10.1. 输入
      2. 2.10.2. 运行结果
      3. 2.10.3. 对比分析
  3. 3. 参考链接