编译原理：算符优先分析

原创文章，转载、引用请注明出处！

今天是个更博的好日子。

写在前面

至此，编译原理实验已经写到第四个实验了。

回想起之前在学期刚开始之前，都说这门课的难度非常之高。现在是教学周第十三周，那么也就没几周就又要进行考试了。要说我对这门课程的看法，那就是“痛并快乐着”。

这门课程的实验，讲实话，是我到目前为止学到的课程的课程实验中最有用的。对我个人而言，只有做了这些实验才明白了到底学了些什么东西。大概上课都在跑神，什么都没听懂233333

而且这些实验的设置对于我这种养成癖好的人来说简直是太有成就感了！第一个实验的结果在之后的实验中都会被用到，这无疑增加了我在进行所有实验时的综合考量：我要把数据结构写成什么样子才能在之后的实验中好用？我要用什么样的方式展示这几次实验之间的关联？这样的话，我每次在写实验的时候，仿佛写的不是一个实验大概是写编译原理这本书233333。这根本就不是一次次无生命的博客写作，而是我倾注了心血的杰作女朋友!

作为一个大三的、今后上学无望的菜鸟，我一直在思考，我把作业写得这样认真到底为了什么（我自认为我的实验代码和文档博客都写的非常认真，至少在我认识的人里面，我的认真程度排前三大概是没有问题）。毕竟成绩对我来说已经不重要了。我还没有寻到答案，姑且就算现在的认真是这种养成和堆砌的成就感带给我的。

做人需要认真，认真就要具象。

做人更要抽象，抽象才会快乐。

努力认真，8懂就问，能快乐多久就快乐多久。

---

目标任务

要求

完成以下描述赋值语句的 LL(1)文法的 LL(1)分析过程。

G[E]:
E→E+T∣E-T∣T 
T→T*F∣T/F∣F
F→(E)∣i

设计说明

终结符号i为用户定义的简单变量，即标识符的定义。

设计要求

• (1)构造该算符优先文法的优先关系矩阵或优先函数;

• (2)输入串应是词法分析的输出二元式序列，即某算术表达式“专题1”的输出结果。输出为输入串是否为该文法定义的算术表达式的判断结果。

• (3)算符优先分析过程应能发现输入串出错。

• (4)设计两个测试用例(尽可能完备，正确和出错)，并给出测试结果;

• (5)考虑编写程序根据算符优先文法构造算符优先关系矩阵，并添加到你的算符优先分析程序中。

---

解答

算符优先分析法

算符优先分析法(Operator Precedence Parse)是仿效四则运算的计算过程而构造的一种语法分析方法。算符优先分析法的关键是比较两个相继出现的终结符的优先级而决定应采取的动作。

算符优先分析法是一种自下而上的分析方法。

该分析法的优点是：简单，有效，适合表达式的分析。而它的缺点有：只适合于算符优先文法，是一个不大的文法类。

算符优先文法

其文法的特点是文法的产生式中不含两个相邻的非终结符。其定义如下：

假定G是不含ε- 产生式的算符文法。对于任何一对终结符a、b，我们说：

• （1）a等于b当且仅当文法G中含有形如P→ ···ab···或P→···aQb···的产生式；

• （2）a小于b当且仅当G中含有形如P→···aR···的产生式，而R(+=>)b···或R(+=>)Qb···；

• （3）a大于b当且仅当G中含有形如P→···Rb···的产生式，而R(+=>)···a或R(+=>)···aQ；

如果一个算符文法G中的任何终结符对（a,b）最多满足下述三个条件之一：

a=b,a<b,a>b

则称G是一个算符优先文法。

设计思想

若想进行算符优先分析，首先我们需要对所给的文法做检查：该文法是否是算符优先文法？

接下来是一系列的准备工作：

（1）对该算符优先文法中的所有非终结符号求FristVT集合；

（2）对该算符优先文法中的所有非终结符号求LastVT集合；

（3）根据所求得的FristVT集合和LastVT集合，构造该算符优先文法的算符优先关系矩阵。

一系列准备工作做完之后，就可根据算符优先分析法的流程对语句进行分析。

检查是否是算符优先文法

算符优先分析法的分析范围仅限于算符优先文法，所以这一步骤是有必要的。

但是，由于是题目所给的文法，在这里可以又省略过这个步骤。

实际上，在进行算符优先关系矩阵的构造时，上述算符优先文法的三条定义都会体现出来。需要我们检查的只是该文法中是否有ε-产生式：显然，该文法是没有ε-产生式的。

构造FristVT集合和LastVT集合

为什么要构造这两个集合？

在前面对算符之间优先级关系的定义中，有一个现象是要去找一个非终结符的首终结符和尾终结符，为了便于计算机操作，定义如下两个概念：

• 首终结符集：FIRSTVT(B） = {b | B → b… 或 B → Cb… }

• 尾终结符集：LASTVT(B) = {b| B → …b 或 B → …bC}

所以，对之前关于算符之间的优先级关系有了新的表示：

• = 关系： A → …ab… 或 A → …aBb…

• < 关系： A → …aB…，对于每一个 b ∈ FIRSTVT(B) ， 都有a < b

• > 关系： A → …Bb…，对于每一个 a ∈ LASTVT(B)，都有 a > b

如何构造这两个集合？

对于文法中的任意非终结符号B，FIRSTVT(B)直接根据定义递归构造：

• （1）若有产生式B→a…或B→Qa…，则 a ∈ FIRSTVT(B)；

• （2）若有产生式P→Q…，则有 FIRSTVT(Q) ∈ FIRSTVT(B)。

同理，LASTVT(B)直接根据定义递归构造：

• （1）若有产生式 B→…a 或 B→…aQ，则 a ∈ LASTVT(B)；

• （2）若有产生式 B→…Q，则有 LASTVT(Q) ∈ LASTVT(B)。

此处需要递归的原因有二：一是该算法需要执行到非终结符号B的FIRSTVT集合或LASTVT集合不再增大为止；二是对于上述定义，两集合的第二条定义都需要其他的非终结符号的FIRSTVT集合或LASTVT集合来帮助构造目标符号B的FIRSTVT集合或LASTVT集合。

对于本次所给的文法，执行上面的构造算法，可得如下结果：

• FirstVT[E] = { ( * + - / i }
• FirstVT[F] = { ( i }
• FirstVT[T] = { ( * / i }
• LastVT[E] = { ) * + - / i }
• LastVT[F] = { ) i }
• LastVT[T] = { ) * / i }

构造算符优先关系矩阵

算符优先分析法的基本原理是：识别句柄并归约。

该分析方法的具体做法是：利用<识别句柄尾，利用>识别句柄头，分析栈存放已识别部分，比较栈顶和下一输入符号的关系，如果是句柄尾，则沿栈顶向下寻找句柄头，找到后弹出句柄，归约为非终结符。

对于所给句子，我们需要时刻查询相邻终结符号的优先关系。此时就需要将各种优先关系存放在一张查询表中，称为算符优先关系矩阵。

算符优先关系矩阵可通过如下步骤构造：

for(每条产生式  P -> X1X2X3...Xn) {
    for(i = 1;i <= n-1; ++i) {
        if(X(i) 和 X(i+1) 均为终结符) {
            X(i) = X(i+1)
        }
        if(i <= n-2 && X(i) 和X(i+2)均为终结符 && X(i+1) 为非终结符) {
            X(i) = X(i+1)
        }
        if(X(i) 为终结符 && X(i+1)为非终结符) {
            for(FIRSTVT(X(i+1))中的每一个元素a) {
                  Xi < a
            }
        }
        if(X(i) 为非终结符 && X(i+1)为终结符) {
            for(LASTVT(X(i))中的每一个元素a) {
                  a > X(i+1)
            }
        }
    }  
}

之前讨论过算符优先文法的检查，这里可以给出一种方法：如果一个文法G按上述算法构造出的优先矩阵是没有重定义项的，文法G是算符优先文法。

对于本次所给的文法，执行上面的构造算法，可得如下结果：

	#	(	)	*	+	-	/	i
#	A	<		<	<	<	<	<
(		<	=	<	<	<	<	<
)	>		>	>	>	>	>
*	>	<	>	>	>	>	>	<
+	>	<	>	<	>	>	<	<
-	>	<	>	<	>	>	<	<
/	>	<	>	>	>	>	>	<
i	>		>	>	>	>	>

根据算符优先关系矩阵进行分析

构造好算符优先关系矩阵之后，便可进行分析。

流程如下：

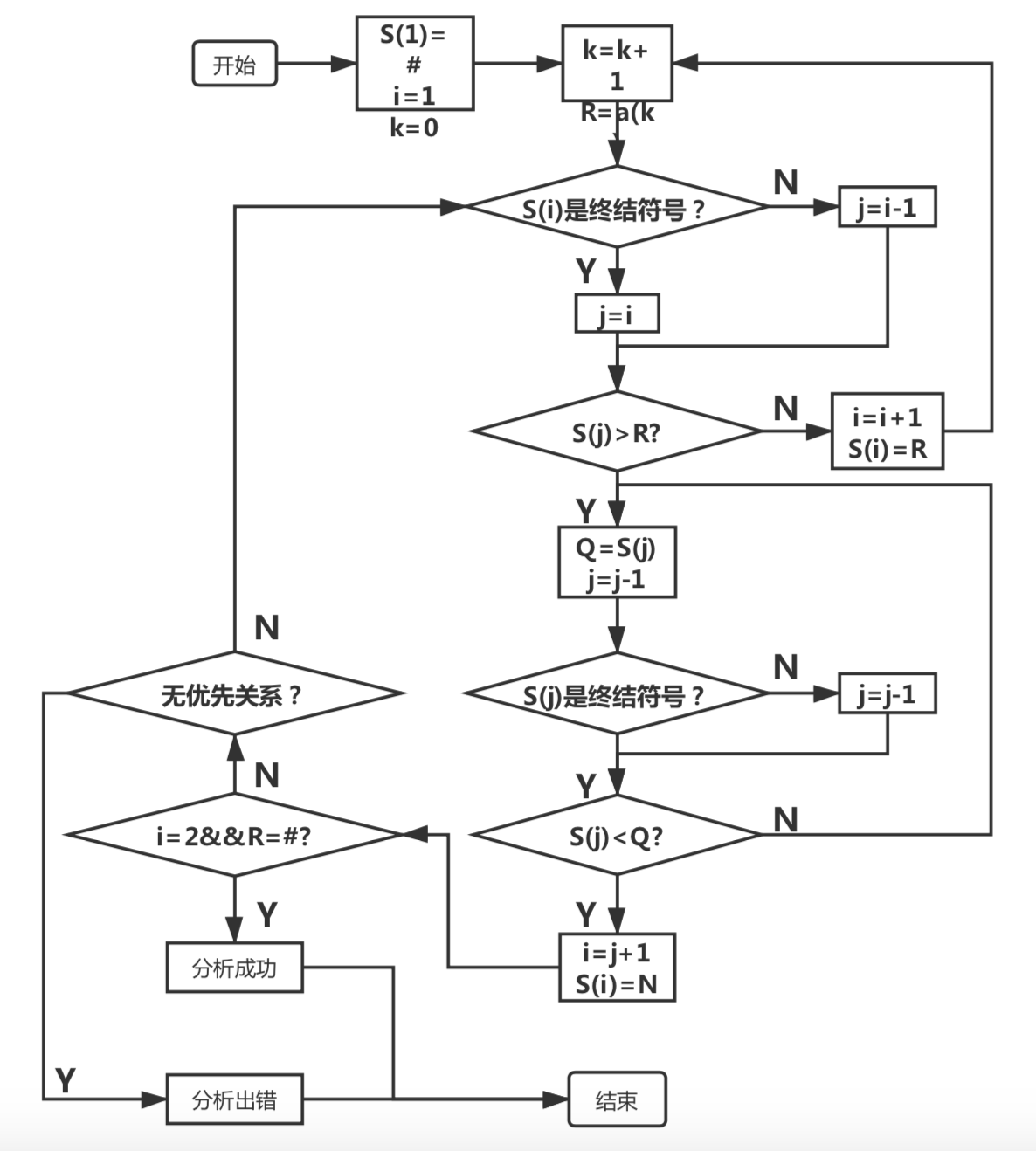
文件结构及函数简介

本专题大部分文件和功能函数与专题1同名，具体的文件结构和功能函数简介见《编译原理：词法分析程序》。

新增文件OPGMatrix.h，内含的函数用作预测分析的准备工作，即求算符优先文法的FirstVT集合、LastVT集合和构造算符优先关系矩阵。

代码分析

详细的主函数流程如下：

int main(int argc, const char * argv[]) {
    //初始化参数
    initAll();
    //读取lab1中输出的二元组结果文件
    readFile_Result();
    //读取lab1中输出的标识符结果文件
    readFile_Identifier();
    //过滤读取结果，得到纯粹的标识符内容
    getPureMorphemeAndSentence();
    //输出过滤后的语句
    printSentenceInfo();
    //读取文法，求得包含所有的非终结符号的不重复集合
    readFile_Formula();
    //求得包含所有的终结符号的不重复集合
    getAllVT();
    //求得文法的FirstVT集合和LastVT集合以及由此构造分析表，并写入txt文件中
    getFirstVT();
    getLastVT();
    //求得算符优先矩阵，并写入txt文件中
    getOPGMatrix();
    writeFile_OPGMatrix();
    //进行分析
    if(getAnalyseResult()){
        cout<<"匹配成功!"<<endl;
        //匹配成功，输出分析栈结果
        printAnalyseResultInfo();
    }else{
        //匹配失败，输出错误位置信息
        cout<<"匹配失败!"<<endl;
        printError();
    }
    return 0;
}

函数getFirstVT()用来求得文法的FirstVT集合。根据FirstVT的构造定义，第一条规则的构造是非常容易理解的，简言之，只要将处在产生式第一个位置的终结符号和处在产生式第二个位置的终结符号（此处第一个位置必须是非终结符号）填入目标非终结符号的FirstVT集合中即可。该规则仅需对所有产生式进行一次遍历即可完成。

而对于第二条规则，则需要借助上一步所求得的所有非终结符号的部分FirstVT集。设置一标志位，进行无限循环：如果在一次循环中，所有的非终结符号中的一个或多个的FirstVT集有扩充，该标志位就被设置为false，代表着还需要进行下一轮的构造。构造停止的标志是：经过上一轮的构造，该文法中的任意非终结符号的FirstVT集均没有再进行扩充。

上述写法避免了递归调用函数，但缺点需要针对两条规则分别设置条件进行循环，且在进行第二条规则的构造之前，必须将第一条规则的内容构造完整且保证正确。

getLastVT()函数同理。

void getFirstVT(){
    //将处在产生式第一个位置的终结符号和处在产生式第二个位置的终结符号（此处第一个位置必须是非终结符号）填入目标非终结符号的FirstVT集合
    for(set<char>::iterator iterVN=VN.begin();iterVN!=VN.end();iterVN++){
        set<char> firstVT;
        for(multimap<char, string>::iterator iterF=Sentence.begin();iterF!=Sentence.end();iterF++){
            if(iterF->first==*iterVN){
                //产生式右部的第一个符号是终结符号
                char ch=iterF->second[0];
                if(!isCaptain(ch)){
                    firstVT.insert(ch);
                }
                //产生式右部的第一个符号是非终结符号
                else{
                    //产生式长度大于2是才做此判断
                    if(iterF->second.length()>1){
                        //产生式右部的第二个符号是非终结符号
                        ch=iterF->second[1];
                        if(!isCaptain(ch)){
                            firstVT.insert(ch);
                        }
                    }
                }
            }
        }
        //将初步构造好的FirstVT集合填入容器中
        FirstVTSet.insert(make_pair(*iterVN, firstVT));
    }
    
    //对第二条规则进行无限循环的构造
    //跳出条件是：经过上一轮的构造，该文法中的任意非终结符号的FirstVT集均没有再进行扩充
    bool ifFindAll=false;
    while(!ifFindAll){
        ifFindAll=true;
        for(multimap<char, string>::iterator iterF=Sentence.begin();iterF!=Sentence.end();iterF++){
            //产生式右部的第一个符号是非终结符号
            if(isCaptain(iterF->second[0])){
                for(map<char,set<char>>::iterator iterFVTS1=FirstVTSet.begin();iterFVTS1!=FirstVTSet.end();iterFVTS1++){
                    if(iterFVTS1->first==iterF->first){
                        for(map<char,set<char>>::iterator iterFVTS2=FirstVTSet.begin();iterFVTS2!=FirstVTSet.end();iterFVTS2++){
                            int len=iterFVTS1->second.size();
                            if(iterFVTS2->first==iterF->second[0]){
                                //B->A...，将A的FirstVT集合合并到B的FirstVT集合
                                iterFVTS1->second.insert(iterFVTS2->second.begin(),iterFVTS2->second.end());
                            }
                            //如果任意非终结符号的FirstVT集合有扩充，更改循环标志位
                            //false代表需要进行下一轮的构造
                            if(len!=iterFVTS1->second.size()){
                                ifFindAll=false;
                            }
                        }
                    }
                }
            }
        }
    }
}

构造算符优先关系矩阵时，按照定义的四个入口进行构造即可。需要注意的是，要对新添规则进行构造：

E' -> 井E井

同时也要在终结符号集合中手动添加井。

void getOPGMatrix(){
    //初始化OPG优先关系矩阵，填上表头
    for(int i=0;i<VN.size()+1;i++){
        for(int j=0;j<VT.size()+1;j++){
            opgMatrix[i][j]="";
        }
    }
    int i=1;
    for(set<char>::iterator iVT=VT.begin(); iVT!=VT.end(); ++iVT) {
        char ch=*iVT;
        opgMatrix[i][0]=ch;
        i++;
    }
    int j=1;
    for(set<char>::iterator jVT=VT.begin(); jVT!=VT.end(); ++jVT) {
        char ch=*jVT;
        opgMatrix[0][j]=ch;
        j++;
    }
    //四个入口
    for(multimap<char, string>::iterator iter=Sentence.begin();iter!=Sentence.end();iter++){
        for(int i=0;i<iter->second.length()-1;i++){
            if(!isCaptain(iter->second[i])){
                if(!isCaptain(iter->second[i+1])){
                    //入口1
                    //X(i) 和 X(i+1) 均为终结符)
                    //X(i) = X(i+1)
                    OPGMatrixInsert(iter->second[i],iter->second[i+1],'=');
                }else{
                    if(i<iter->second.length()-2&&!isCaptain(iter->second[i+2])){
                        //入口2
                        //i <= n-2 && X(i) 和X(i+2)均为终结符 && X(i+1) 为非终结符
                        //X(i) = X(i+2)
                        OPGMatrixInsert(iter->second[i],iter->second[i+2],'=');
                    }
                        for(map<char, set<char>>::iterator iter_aA=FirstVTSet.begin();iter_aA!=FirstVTSet.end();iter_aA++){
                            if(iter->second[i+1]==iter_aA->first){
                                for(set<char>::iterator ins=iter_aA->second.begin();ins!=iter_aA->second.end();ins++){
                                    //入口3
                                    //X(i) 为终结符 && X(i+1)为非终结符
                                    //Xi < a
                                    OPGMatrixInsert(iter->second[i],*ins,'<');
                                }
                            }
                        }
                    
                }
            }else{
                if(!isCaptain(iter->second[i+1])){
                    for(map<char, set<char>>::iterator iter_Aa=LastVTSet.begin();iter_Aa!=LastVTSet.end();iter_Aa++){
                        if(iter->second[i]==iter_Aa->first){
                            for(set<char>::iterator ins=iter_Aa->second.begin();ins!=iter_Aa->second.end();ins++){
                                //入口4
                                //X(i) 为非终结符 && X(i+1)为终结符
                                //a > X(i+1)
                                OPGMatrixInsert(*ins,iter->second[i+1],'>');
                            }
                        }
                    }
                }
            }
        }
    }
    //单独对#做处理:E'->#E#
    // # < FirstVT(E)
    for(map<char, set<char>>::iterator iter_aA=FirstVTSet.begin();iter_aA!=FirstVTSet.end();iter_aA++){
        if(Begin==iter_aA->first){
            for(set<char>::iterator ins=iter_aA->second.begin();ins!=iter_aA->second.end();ins++){
                OPGMatrixInsert('#',*ins,'<');
            }
        }
    }
    // LastVT(E) > #
    for(map<char, set<char>>::iterator iter_Aa=LastVTSet.begin();iter_Aa!=LastVTSet.end();iter_Aa++){
        if(Begin==iter_Aa->first){
            for(set<char>::iterator ins=iter_Aa->second.begin();ins!=iter_Aa->second.end();ins++){
                OPGMatrixInsert(*ins,'#','>');
            }
        }
    }
    //#和#的关系为ACC
    OPGMatrixInsert('#','#','A');
}

最后，算符优先分析算法完全按照上面的流程图进行构造。不再赘述。

结果测试

首先依据所给文法写出一正确的语句：

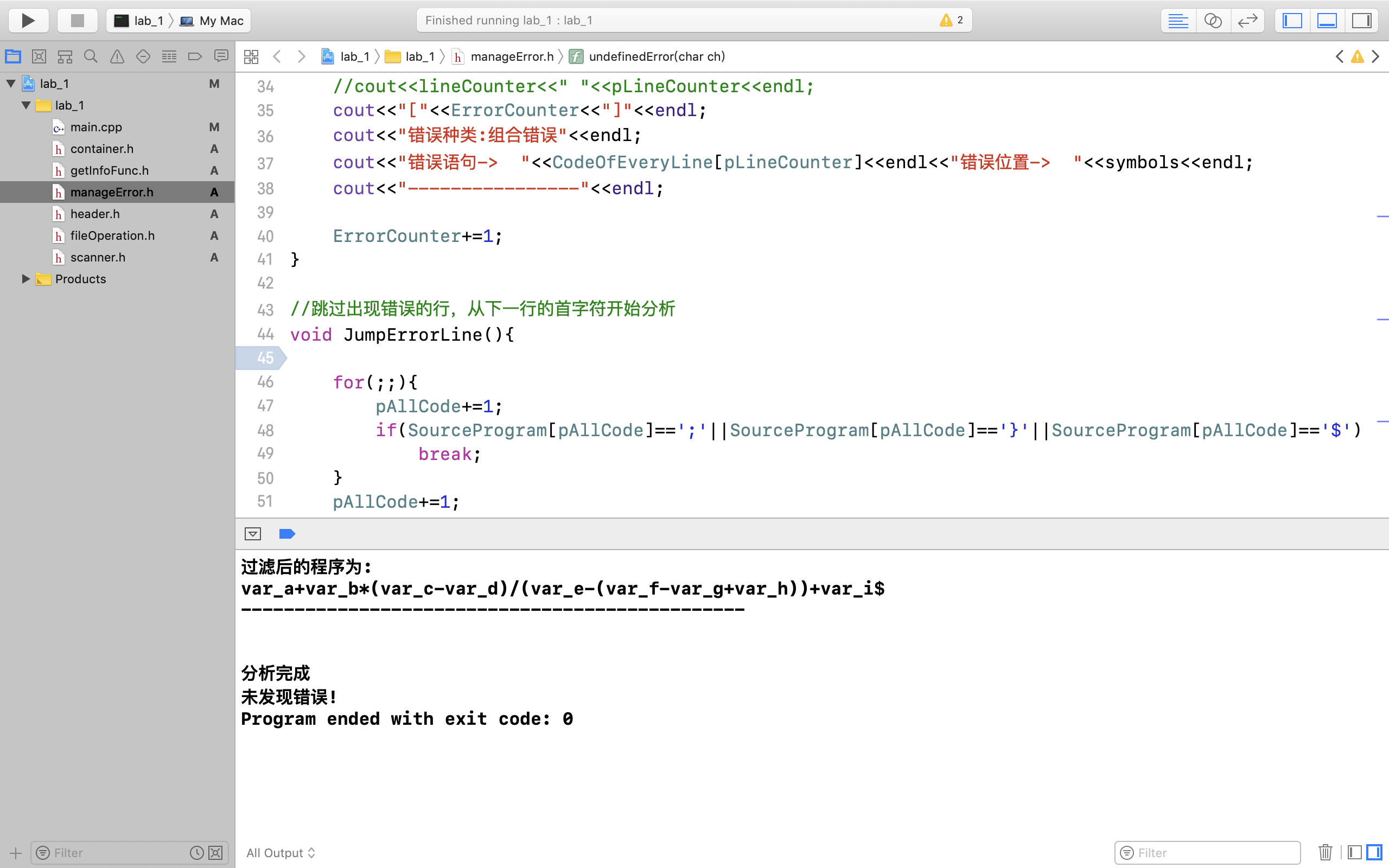
var_a+var_b*(var_c-var_d)/(var_e-(var_f-var_g+var_h))+var_i

将此表达式写入专题1中的SourceProgram.txt文件，运行专题1程序：

查看标识符文件Identifier.txt：

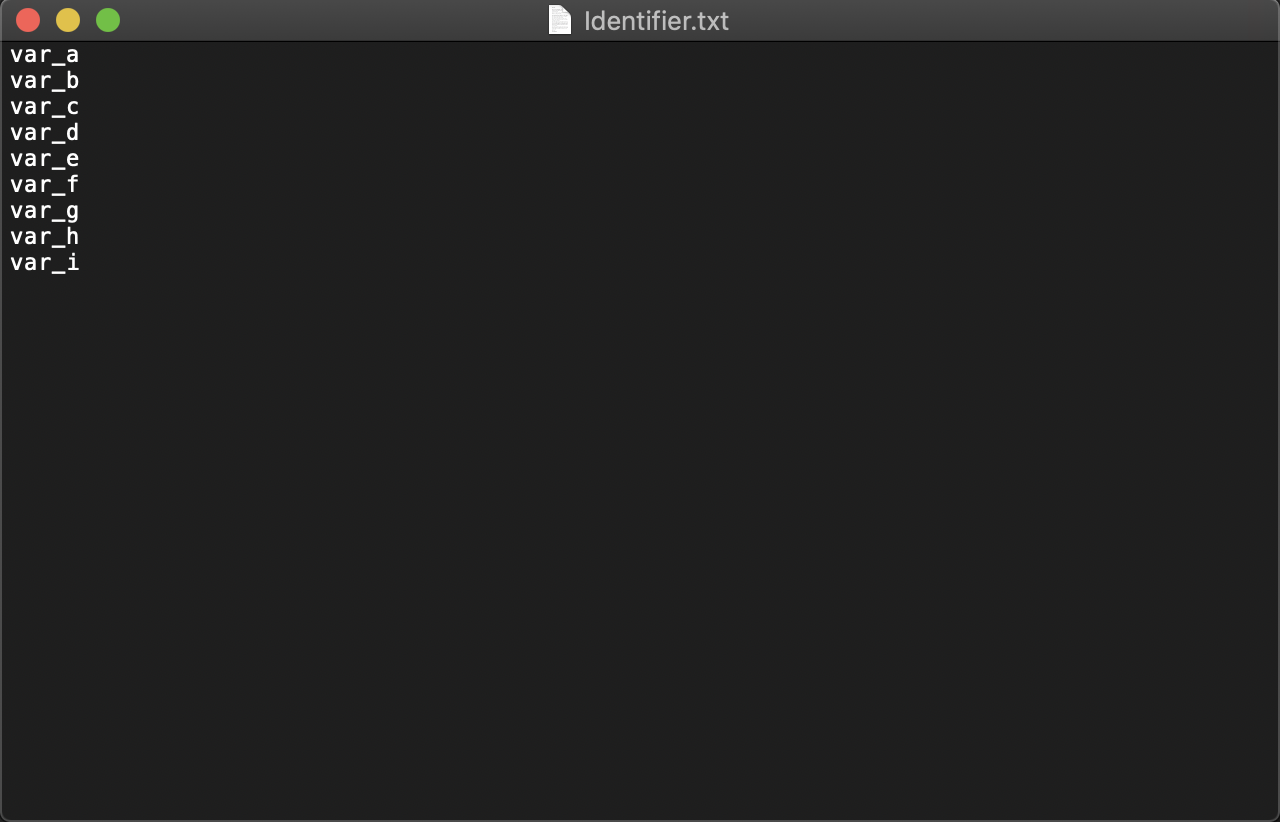
查看词素二元组文件ResultofLexicalAnalysis.txt：

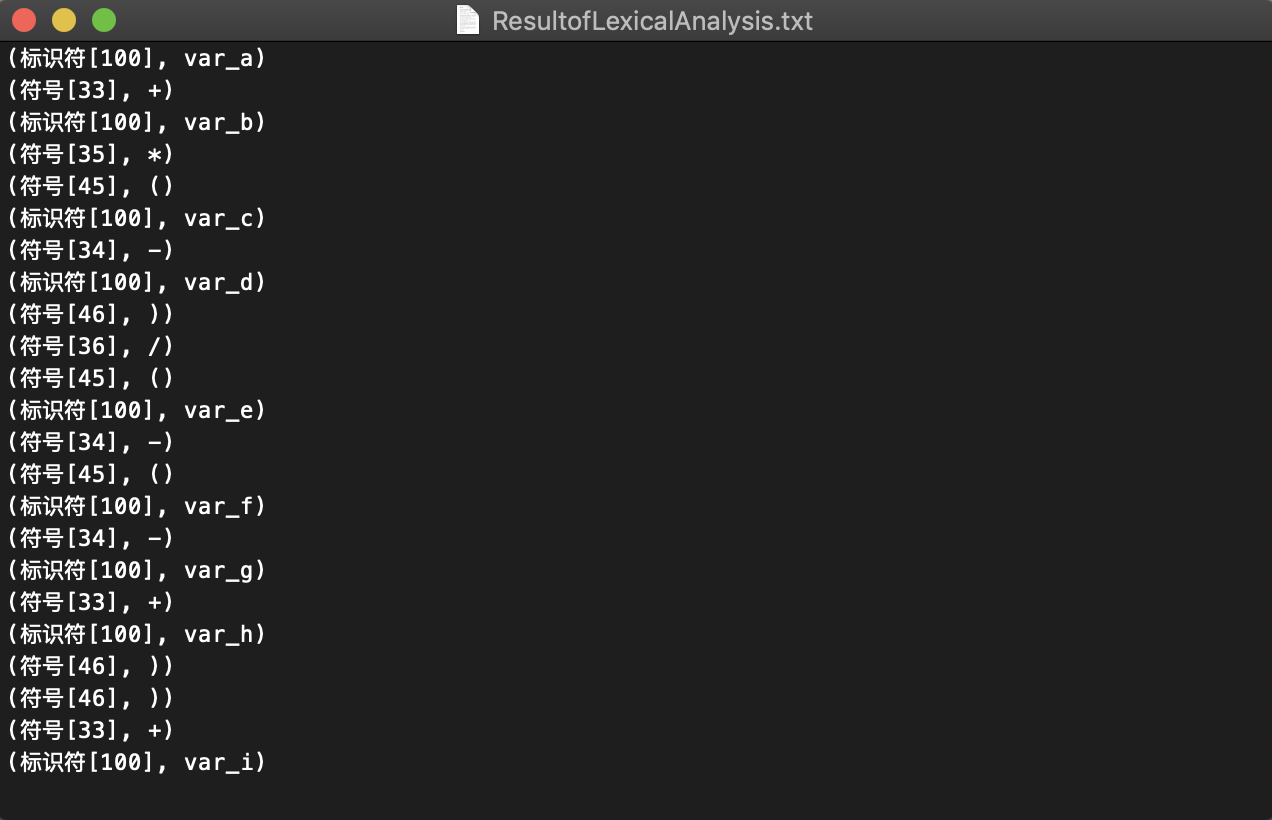
可以看到对于专题1来说，上述语句是符合要求的。

接下来运行本专题的算符优先分析程序：

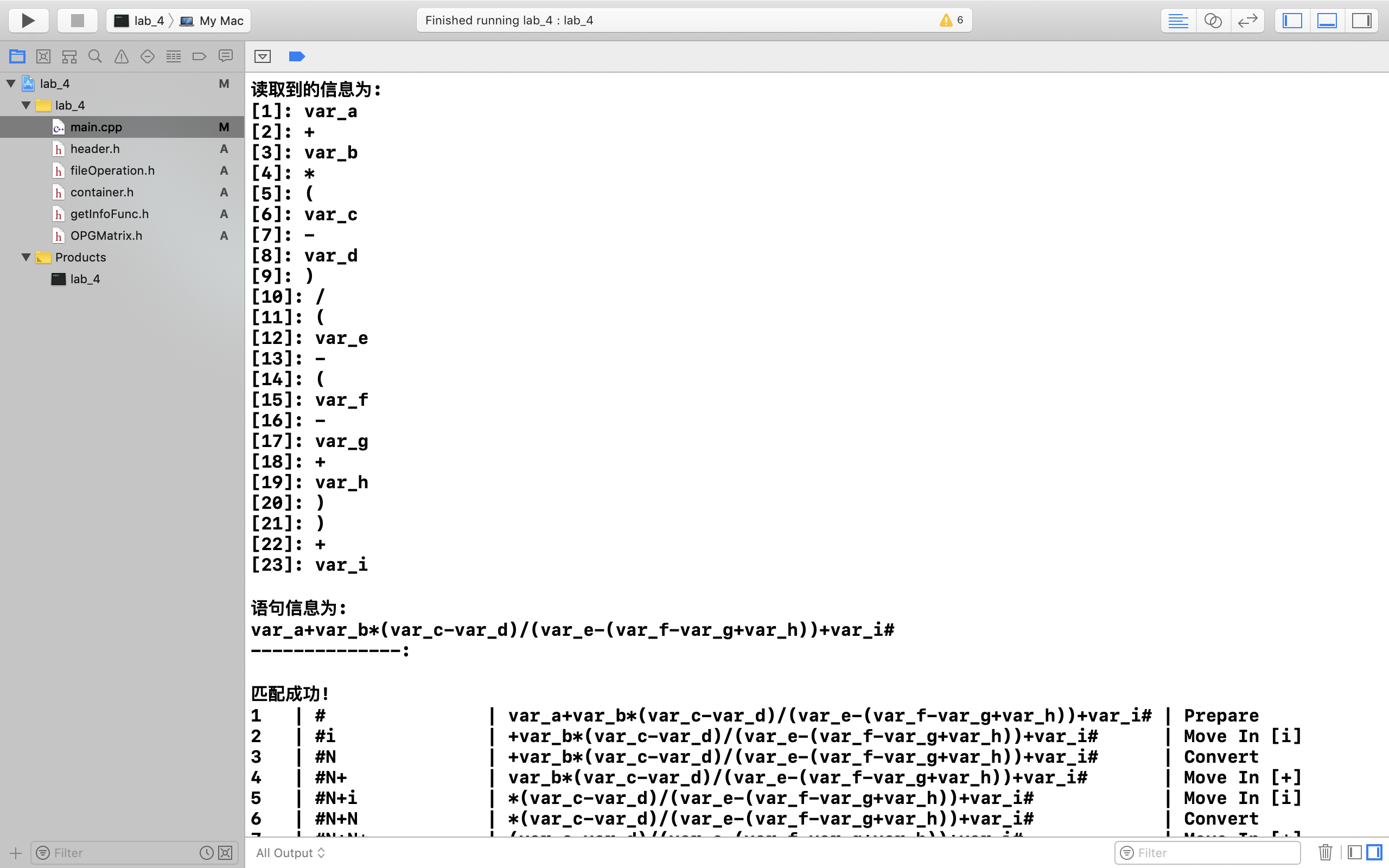
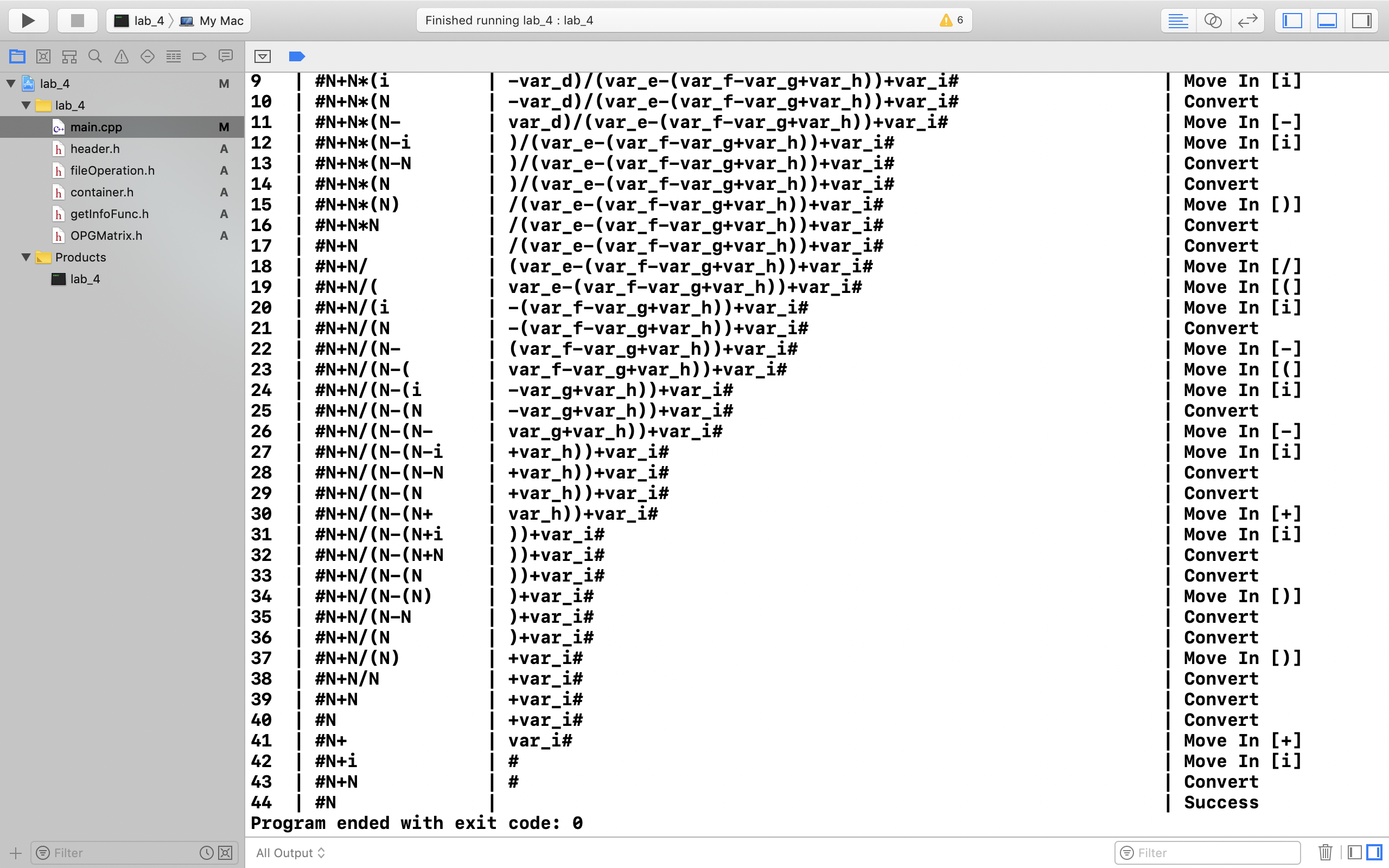
查看生成的算符优先文法矩阵文件OPGMatrix.txt：

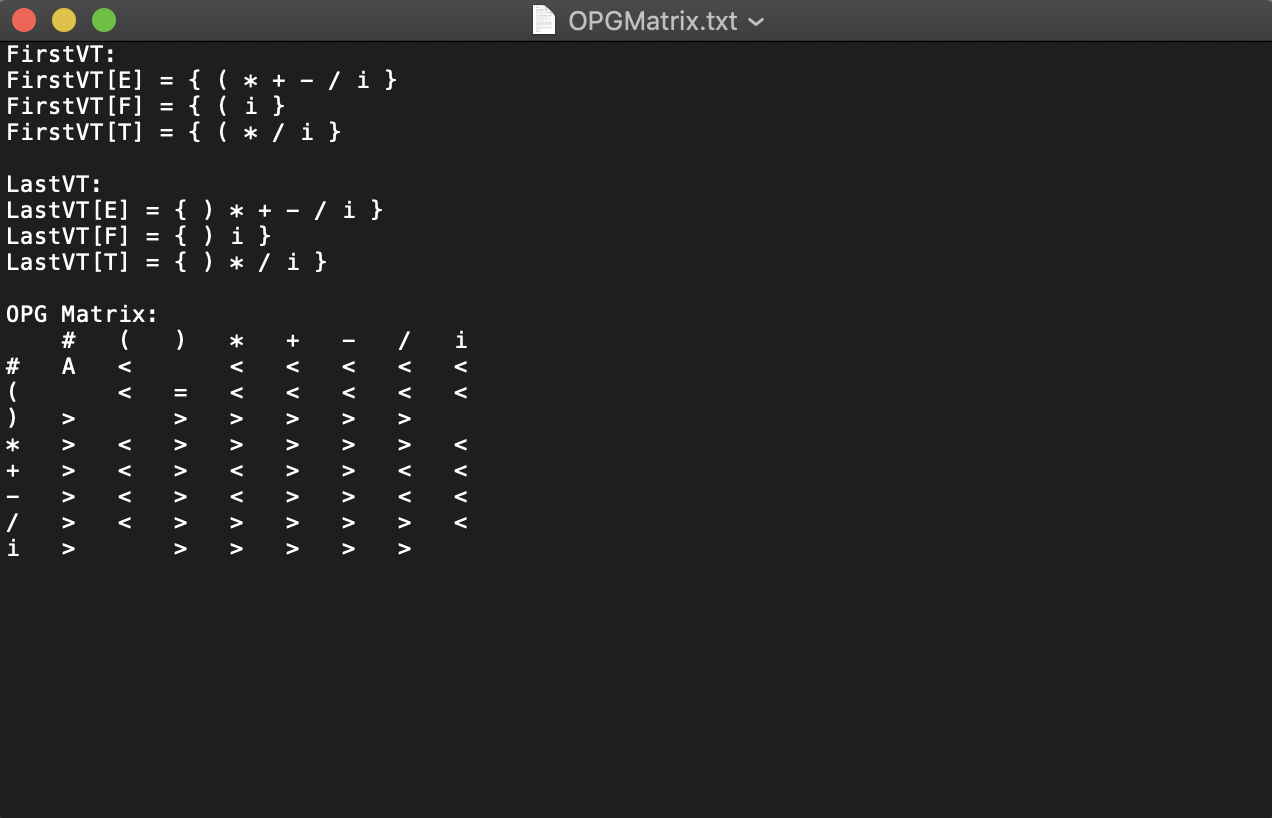
上述测试结果证明了两个程序可按设计本意顺利完成各项功能。

接下来，修改我们所给出的正确的语句，使它变得”错误”。当然这里所说的错误指的是在本专题的情景下是错误的。这些语句无论如何修改，都必须符合专题1的情景。

• var_a = var_b*(var_c-var_d)/(var_e-(var_f-var_g+var_h))+var_i

标示出来的是我们添加的错误。

对如上情形进行测试：

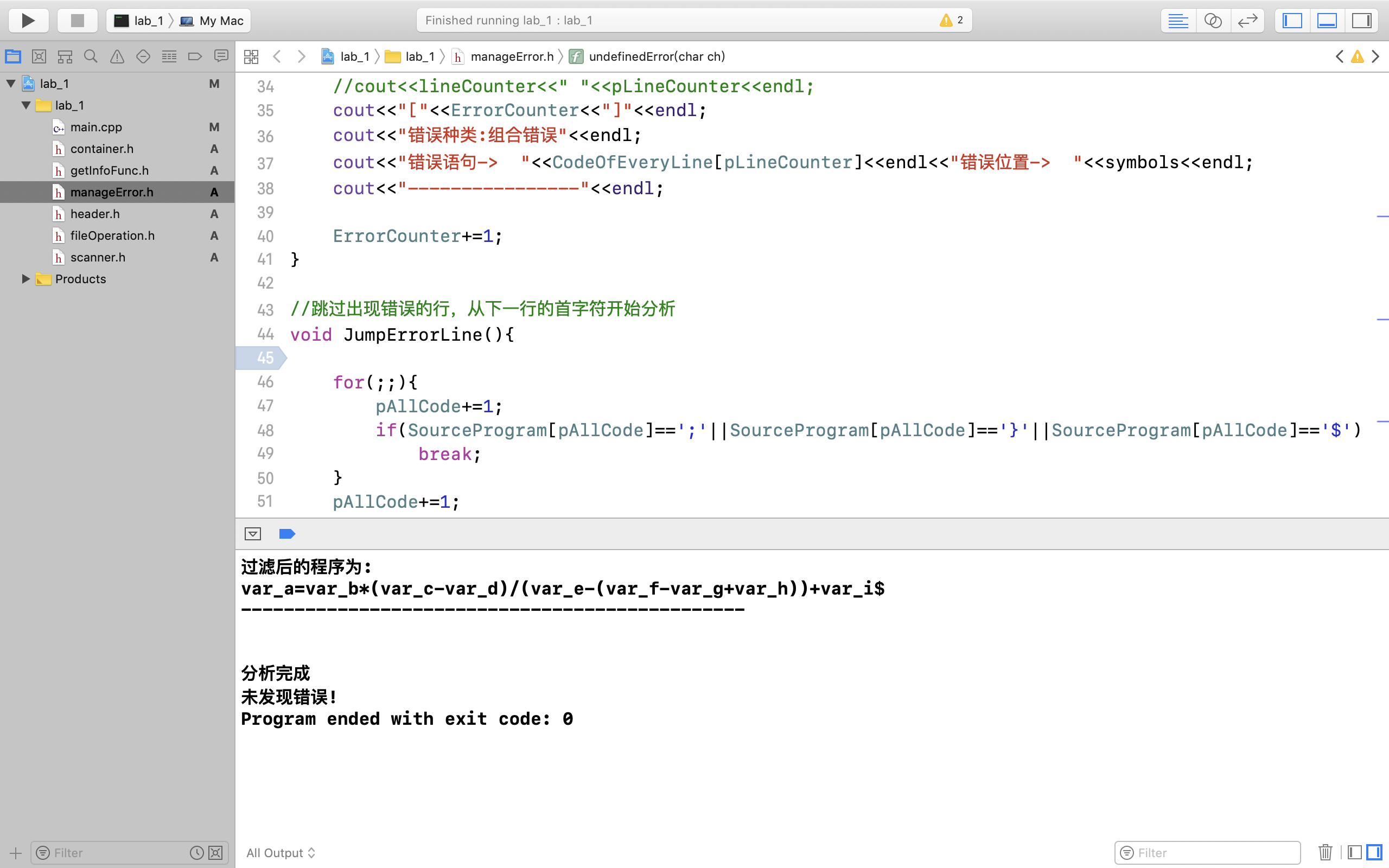
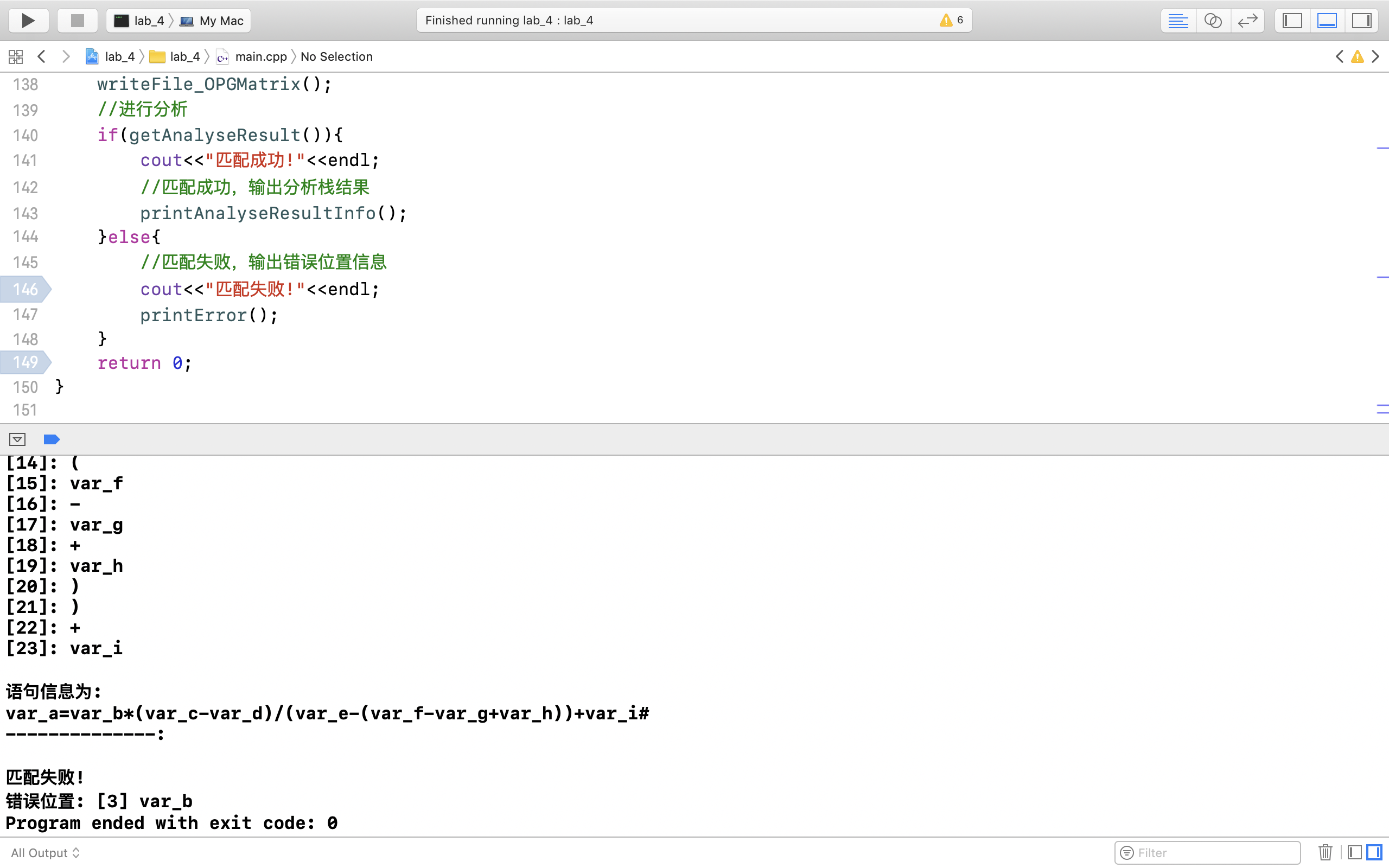
根据上述结果可以看出，本程序可以实现所给算符优先文法的分析，并能指出具体错误的位置。