原创文章，转载、引用请注明出处！

题目

包装生产线的质量检测：一家用瓶子装各种工业化学品的装瓶公司听说你成功解决了成像问题，并雇佣你设计一种检测瓶子未装满的方法。当瓶子在传送带上运动，并通过自动装填机和封盖机进行包装时有如下图所示的情景。当液体平面低于瓶颈底部和瓶子肩部的中间点时，认为瓶子未装满。瓶子的横断面上的倾斜部分及侧面定义为瓶子的肩部，瓶子在不断移动。公司有一个图像系统，装备了有效捕捉静止图像的前端闪光照明设备。所以你可以得到非常清晰的图像。基于以上你得到的资料，提出一种检测未完全装满的瓶子的解决方案。清楚地表述你做的所有设想和很可能对你提出的解决方案产生影响的假设。并实现它。

说明

所选用的编程语言为python3.6；
编译环境：
Jupyter Notebook（此前被称为 IPython notebook）是一个交互式笔记本，支持运行 40 多种编程语言。
Jupyter Notebook 的本质是一个 Web 应用程序，便于创建和共享文学化程序文档，支持实时代码，数学方程，可视化和markdown。用途包括：数据清理和转换，数值模拟，统计建模，机器学习等等。

搭载在Anaconda上的Jupyter Notebook

实现

问题分析

本问题的核心需求是检测图片中未满足要求的部分并标出。

首先，什么部分是“未满足要求”的部分？根据题意我们可以定义：每一个没有装满的容器会被视为未满足要求的部分。

接下来的问题是，“没有装满”的容器指的是什么样的容器？或者换一个问法：什么样的容器是合格的？对于我们来说，我们可以很轻松的判断出来，没有装满的容器是所给图片中间的那一个，而其余四个容器仅有瓶口部分是没有装满的，这样的容器我们把它视作合格。

没有装满（不合格）的容器

根据上面的标注，我们可以找到一个最明显的标志：未合格容器的空白部分明显比合格部分的空白面积大。分析到此，此题的核心需求就变成了：求出每一个容器未装满部分在图片中的面积，并将高于正常值的容器指出。

假设

根据问题分析和题目标注，需要先针对所给情景作出如下断言和假设：

原题中叙述：“公司有一个图像系统，装备了有效捕捉静止图像的前端闪光照明设备。所以你可以得到非常清晰的图像”，由此断言：所得图像的质量稳定的，即图像大小和图像内容分布（容器在图片中的相对位置）是不变的；
所给的图片中仅有中间的一个容器所装的液体是明显不足的，其他四个容器的液体平面是一样高的，由此假设：其余四个容器为合格的产品，它们在瓶口处的空余部分是正常的。这一假设非常重要，它将帮助我们定义不合格产品的阈值。

图像对象检测

本问题所属的问题大类为图像对象检测：图像对象检测是利用图像处理与模式识别等领域的理论和方法，从图像中定位感兴趣的目标，需要准确地判断每个目标的具体类别，并给出每个目标的边界框。

对于本情景而言，所给图像为灰度图像，若想从这一角度来探索问题的解决方法，最容易想到的思想就是二值化。

在数字图像处理中，二值图像占有非常重要的地位，图像的二值化使图像中数据量大为减少，从而能凸显出目标的轮廓。本体背景和所检测部位已经分别是黑白两色，非常适合这个思路。

读取图像
首先介绍本程序主要用到的py包： scikit-image（aka skimage）是图像处理和计算机视觉算法的集合。主要的软件包skimage提供了一些用于在图像数据类型之间转换的实用程序。

导入文件包，读取图像，输出结果

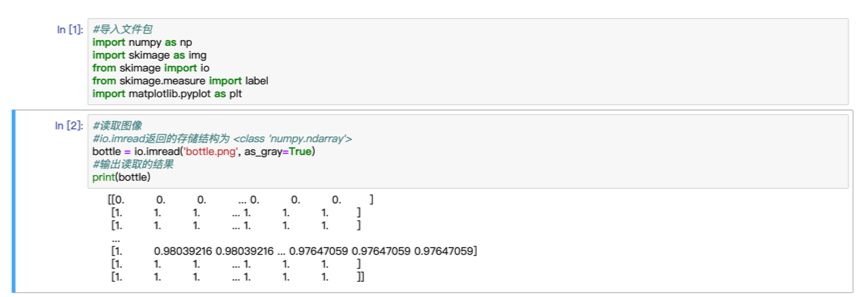
读取图像，输出图像结果，可以看到，imread函数会将图像按照行列存储为二维数组，且是归一化的灰度图。

输出读取结果及图像大小

输出图像及其大小，验证是否读取正确。

图像文件信息

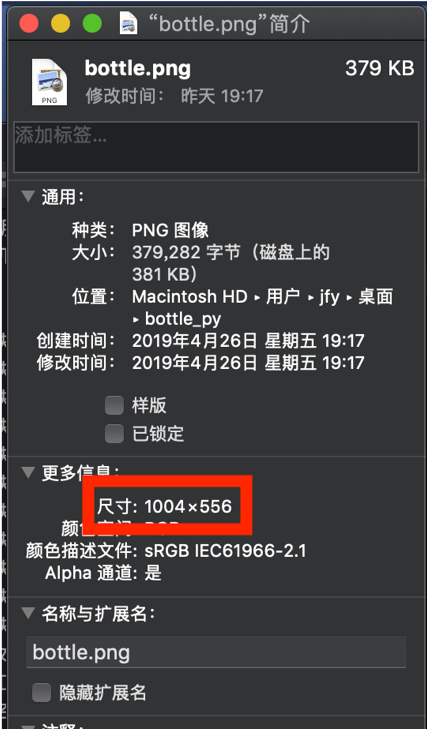
输出的大小为（556，1004），再查看图片文件，发现可以匹配，同时说明该数据结构是按照像素的行列进行读取和存储的。

二值化

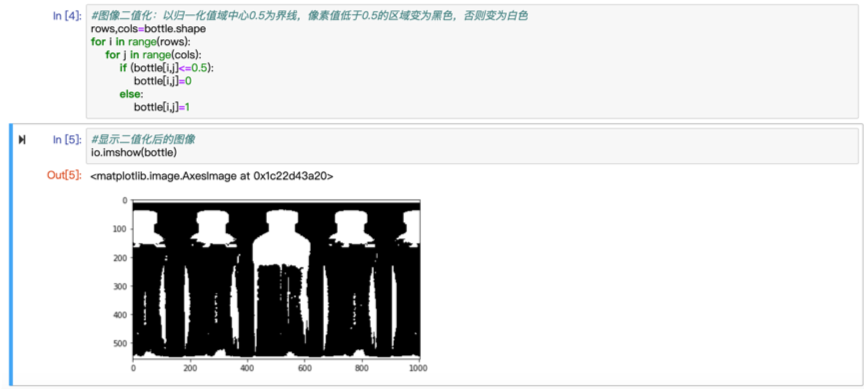
对图像进行二值化：以归一化值域中心0.5为界线，像素值低于0.5的区域变为黑色，否则变为白色。

图像二值化

图像无用部分处理

二值化后的图像

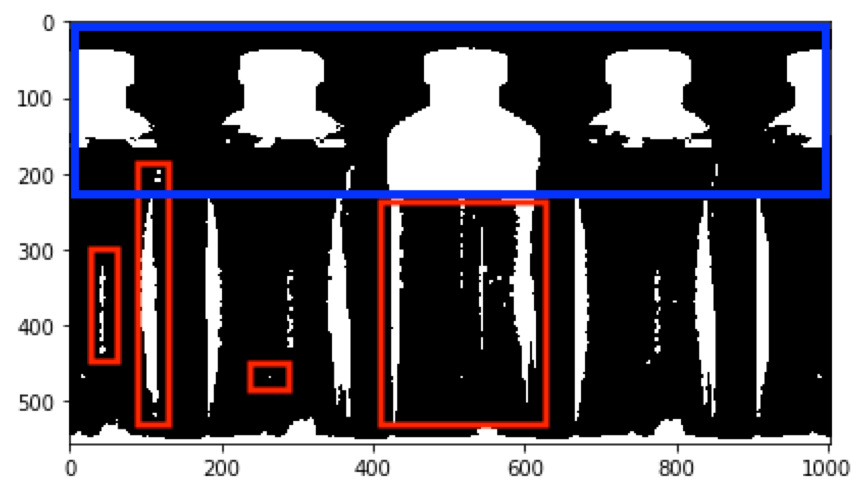
二值化后的图片如上所示，可以看出，即使对图片进行了二值化，我们想要关注的部分的轮廓也并不是非常清晰的：蓝色标记才是我们想要关注的部分，但是还有很多其他的没有被处理为背景的部分（红色标记）也出现在图中，这些部分很可能是容器侧壁的反光造成的。尤其是对于中间未合格的容器来说，它的空余部分下面还有一部分侧壁的空白与之相连，这样就造成了所要检测的区域和无关区域一同构成了连通域。

很容易明晰的一点是：我们说某一个容器所装的液体量不合格，意思是只要该容器有很小的该装液体的部分被检测到没有装液体，至于该不合格产品到底少装了多少，我们并不关心。所以我们只要看容器从瓶口部分及其往下面衍生的一部分即可，至于瓶体的下半身完全可以不用检测。

基于此，我们对该图像的无用区域进行切割和处理：按照4:6的比例分割图像，并把下60%部分舍去，直接作为背景。

二值化图像无用部分处理

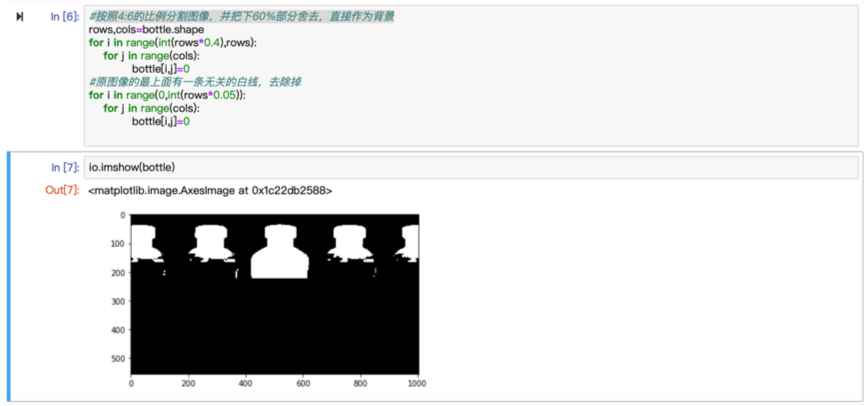
连通域

根据上述处理结果，我们就可以很明显的看出合格品和不合格品差别了。接下来，我们需要对图片中的每一块白色部分的面积做统计，这些白色部分在数字图像处理中被统称为“连通域”。

首先使用skimage.measure的字函数label获取连通域信息。这个函数的作用是：输入二值化后的数字图像矩阵，返回的内容为连通域的个数和带有连通域标记的矩阵。对于每一个连通域，都为他们赋予一个整数值。

输出的数量为16，则我们可以知道，该图像中共有17个连通域，出去编号为0的黑色背景，共有16个白色的区域，它们的编号为1-16。

输出连通域信息：无排序

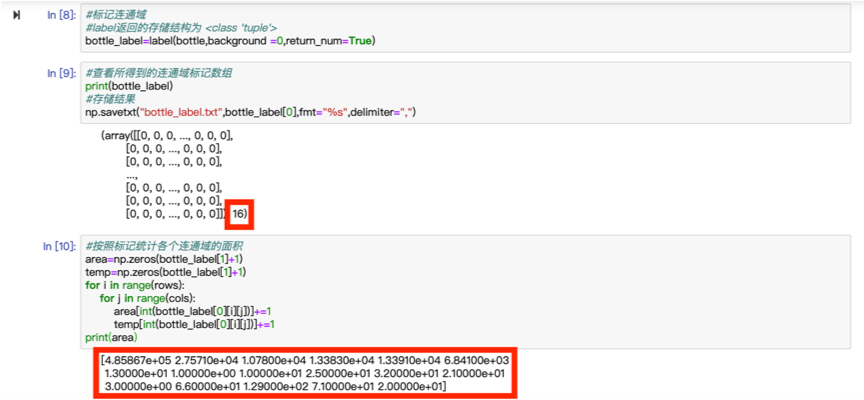
将各连通域面积进行排序输出：

输出连通域信息：排序后

数据如下：

[1.0000e+00 3.0000e+00 1.0000e+01 1.3000e+01 2.0000e+01 2.1000e+01
 2.5000e+01 3.2000e+01 6.6000e+01 7.1000e+01 1.2900e+02 6.8410e+03
1.0780e+04 1.3383e+04 1.3391e+04 2.7571e+04]

再根据我们对于图片内容的观察，我们可以很容易的从数据中推断出一些内容：最大的数2.7571e+04代表了不合格区域的面积，即中间的容器，接下来的4个数6.8410e+03、1.0780e+04、1.3383e+04、1.3391e+04代表了四个合格容器，而在这四个数中，6.8410e+03与另外三个数不在一个数量级上的原因是：它代表了最右边那个不完整的合格容器。1.0780e+04比6.8410e+03稍大一些，从图中可以看出它代表了最左边那个不完整的合格容器。

剩下的两个数1.3383e+04、1.3391e+04非常接近，我们便可由此断言：合格容器的空白部分上限就在这两个值附近。在这里，我们定义了判断是否合格的阈值。

过滤无关连通域

上面分析了有用的值，剩下的值很明显就是无用的，因为我们在图中仅有上述5个区域需要进行判断，那么其余的连通域就是无关的连通域。我们需要将这些连通域处理为背景。

在进行上述处理前，需要先得到排序过后的面积和原面积数组的映射关系：

排序映射

接下来，过滤无关连通域：

过滤无关连通域

判断并得到结果

先来查看过滤后的结果，为不同标记的连通域赋予不同的颜色，背景依旧为黑色：

过滤无关连通域之后的结果

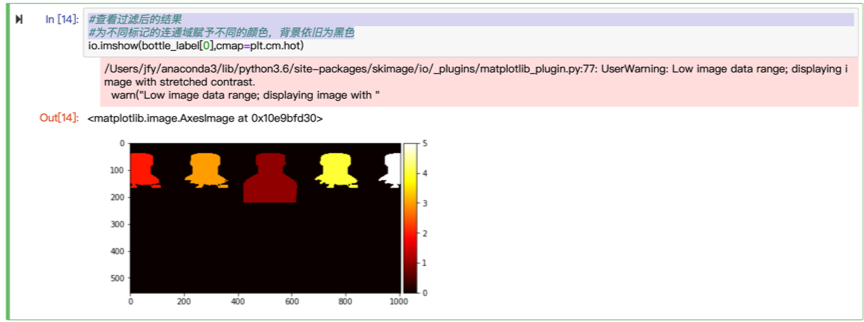
可以看到，需要被判断的5个连通域都被我们用不同的标记给出了。接下来，只需要用我们在上面给出的阈值对每个连通域进行判断即可。

对连通域的面积进行判断

查看判断后的最终结果：

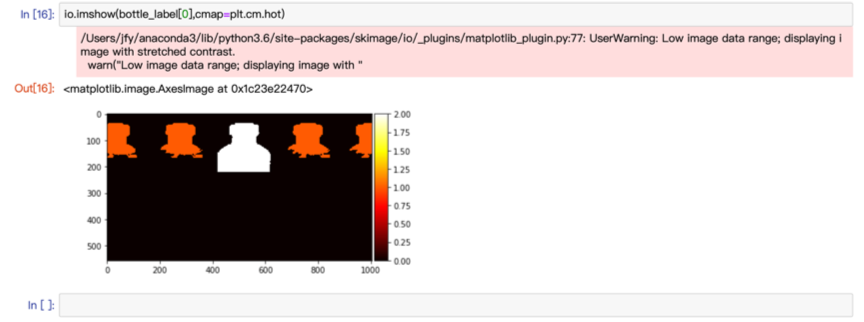
Optional title
最终结果

可以看到，正确的部分被彩色填充，错误的部分依旧是白色的。

将这个结果和我们在一开始时对于图片的判断进行对比，发现结果完全正确，我们的程序可以达到预期的结果。

附录：代码

#导入文件包
import numpy as np
import skimage as img
from skimage import io
from skimage.measure import label
import matplotlib.pyplot as plt

#读取图像
#io.imread返回的存储结构为 <class 'numpy.ndarray'>
bottle = io.imread('bottle.png', as_gray=True)
#输出读取的结果
print(bottle)

#显示所读取的图像信息
print("size: ")
print(bottle.shape)
io.imshow(bottle)

#图像二值化：以归一化值域中心0.5为界线，像素值低于0.5的区域变为黑色，否则变为白色
rows,cols=bottle.shape
for i in range(rows):
    for j in range(cols):
        if (bottle[i,j]<=0.5):
            bottle[i,j]=0
        else:
            bottle[i,j]=1
#显示二值化后的图像
io.imshow(bottle)

#按照4:6的比例分割图像，并把下60%部分舍去，直接作为背景
rows,cols=bottle.shape
for i in range(int(rows*0.4),rows):
    for j in range(cols):
            bottle[i,j]=0
#原图像的最上面有一条无关的白线，去除掉
for i in range(0,int(rows*0.05)):
    for j in range(cols):
            bottle[i,j]=0
io.imshow(bottle)

#标记连通域
#label返回的存储结构为 <class 'tuple'>
bottle_label=label(bottle,background =0,return_num=True)

#查看所得到的连通域标记数组
print(bottle_label)
#存储结果
np.savetxt("bottle_label.txt",bottle_label[0],fmt="%s",delimiter=",")

#按照标记统计各个连通域的面积
area=np.zeros(bottle_label[1]+1)
temp=np.zeros(bottle_label[1]+1)
for i in range(rows):
    for j in range(cols):
        area[int(bottle_label[0][i][j])]+=1
        temp[int(bottle_label[0][i][j])]+=1
print(area)

#按对连通域的面积进行从小到大排序
temp=temp[1:]
temp.sort()
#查看排序后的数组
print(temp)

#将排序后前的数组顺序映射到排队后的数组
area_sort_num=np.zeros(bottle_label[1])
for i in range (bottle_label[1]):
    for j in range (1,bottle_label[1]+1):
        if(int(temp[i])==int(area[j])):
            area_sort_num[i]=j
            break
#查看结果
print(area_sort_num)

#过滤无关的连通域

#a：过滤阈值b在排序前数组中的位置映射，用来做循环
a=-1
#过滤的阈值b：如果连通域面积小于b，则会被视作背景
b=(1.2900e+02)+1
#寻找b的值，赋给a
for i in range(len(temp)):
    if(temp[i]>b):
        a=i;
        break;
#过滤掉无关的连通域面积，使之成为背景
for i in range(rows):
    for j in range(cols):
        for k in range(a):
            if(int(bottle_label[0][i][j])==area_sort_num[k]):
                bottle_label[0][i][j]=0

#查看过滤后的结果
#为不同标记的连通域赋予不同的颜色，背景依旧为黑色
io.imshow(bottle_label[0],cmap=plt.cm.hot)

#a：过滤阈值b在排序前数组中的位置映射，用来做循环
d=[]
#过滤的阈值b：如果连通域面积小于b，则会被视作背景
c=(1.2900e+02)+1
#寻找b的值，赋给a
for i in range(len(temp)):
    if(temp[i]>1.3391e+04):
        d.append(i);
        break;

for i in range(rows):
    for j in range(cols):
        for k in range(a):
            for k in range(len(d)):
                if(int(bottle_label[0][i][j])==area_sort_num[d[k]]):
                    bottle_label[0][i][j]=2
                elif(int(bottle_label[0][i][j])!=0):
                    bottle_label[0][i][j]=1
io.imshow(bottle_label[0],cmap=plt.cm.hot)