原创文章,转载、引用请注明出处!
写在前面
时间长没有深度学习的新博客了,这也快到假期了,这门课程的学习还是得捡起来。
在此之前一直在考虑一个问题:这门纯属自学的课程,我要按照什么样的方式或者顺序去学呢?想来想去最好的方法还是找一本教科书,按照教科书的内容去学,会比我个人从百度上以查找的方式和联想今天自己该学什么内容这样子会好一些。在此先挂上我所选用的教科书的信息。教科书以后说不定是会换的,但是现阶段还是打算照着这本书的目录进行学习。


本章前言
大多数进行深度学习或者机器学习的人有极大概率接触过MINST手写数据集。
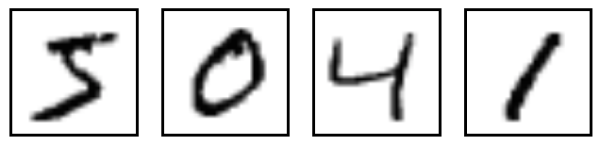
这个数据集在这类课程中的地位大概就和在学习编程语言的时候进行的第一次控制台输出的”hello world!“一样。
本章的目的,就是通过实现手写数字识别的神经网络,来好好了解一下什么是深度学习。
感知器
什么是神经网络?神经网络由什么组成?它如何进行工作?
首先解释一种被称为“感知器”的人工神经元:一个感知器接受一个或多个二进制输入,给出一个二进制输出。对于每一个输入,给予权重表示该输入相对于输出的重要性。神经元的输出为二值输出,由其阈值决定,该阈值也是神经元的一个参数。
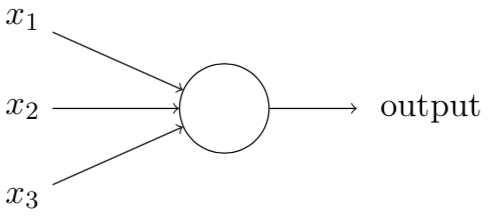
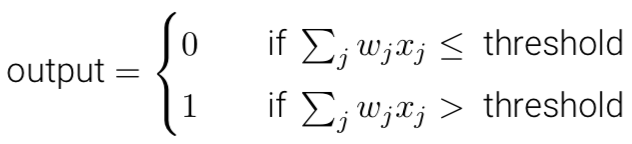
可以将上述感知器看作依据权重来做出决定的设备。随着权重和阈值的变化,将得到不同的“设备”(决策模型)。但单个感知器并不可能用来做出全部的决策,因为决策往往是复杂的,是多元的。既然单个感知器做不到这样的事情,那么我们就用多个感知器如何?看看下面的感知器网络:
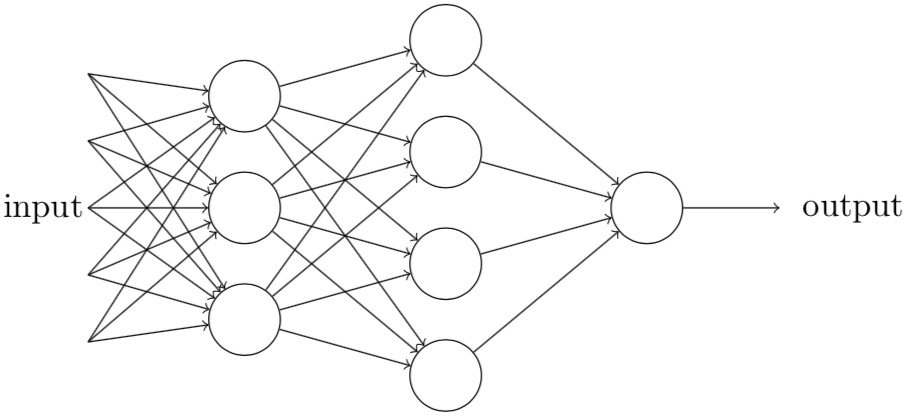
在这个网络中,每一层网络都能比前一层网络考虑的内容更复杂。换言之,每一层网络都比前一层网络考虑了更多的细节。实际上我们完全可以用感知器来实现任何逻辑功能,即与或非的运算。这说明感知器的运算是具有通用性的,但从另外一个方向考虑,难道我们不是在学习一种新的逻辑计算设备?不过实际情况就是这样,只不过是感知器区别于一般的逻辑计算设备的思路是我们可以设计我们自己的学习算法,来自动调整人工神经元的权重和偏置(阈值),这一点是非常非常非常重要的。
最后,简化感知器的数学描述,两个变动:将求和写为向量的点乘、将感知器的阈值(-threshold)用偏置b代替。
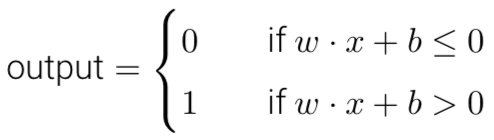
S型神经元
学习算法看上去也太理想太好用了,那么如何实现神经元的学习算法?
假设我们有一个感知器网络来帮助我们进行手写数字图像的分类。我们希望该网络能自动的学习权重和偏置,来提高正确分类的成功率。为了看清楚这个网络是怎样的学习的,我们常规的做法是把网络中的参数作微小的改动。如果这个微小的改动对于网络的结果输出的影响是巨大的,那么我们就能让学习算法变得可能。
一个例子:假如你的网络总会把8错误的认为成9,那么我们可以通过反复的进行细微改动网络参数,使8越来越容易被识别成8,这时,我们就说这个网络在进行学习。
但实际上这个想法里有很大的问题:网络中单个感知器上一个权重或偏置的微小改动有时候会引起那个感知器的输出完全翻转,如0变到1。这样的翻转可能接下来引起其余网络的行为以极其复杂的方式完全改变。
抓工作不能狗熊掰棒子,去过的每个地方都要抓反馈。——摘自习近平参加十二届全国人大四次会议湖南代表团审议的讲话,2016年3月8日。
因此,虽然8可能被正确分类,但网络在其它图像上的行为很可能以一些很难控制的方式被完全改变。这么做,8是分对了,那么012345679呢?这使得逐步修改权重和偏置来让网络接近期望行为变得困难。
对于上述问题,引入S神经元来解决问题:S型神经元和感知器类似,不同是S型神经元受整个网络的微小偏置和改动的影响是较小的。
使用和感知器相同的方式可描述S型神经元,它们都是多输入单输出的单元。它们之间的区别是:感知器的输入输出都是二值的,而S型神经元的输入不是二值的,它的每一个输入是介于[0,1]的一个值。同样的,S型神经元也有用来描述重要性的权重$w$和描述阈值的偏置$b$。
其输出也不是0和1,变为:σ(w·x+b),其中σ被称为sigmoid函数(sigmoid函数具体是什么不重要,重要的是这个函数绘制出来的形状):
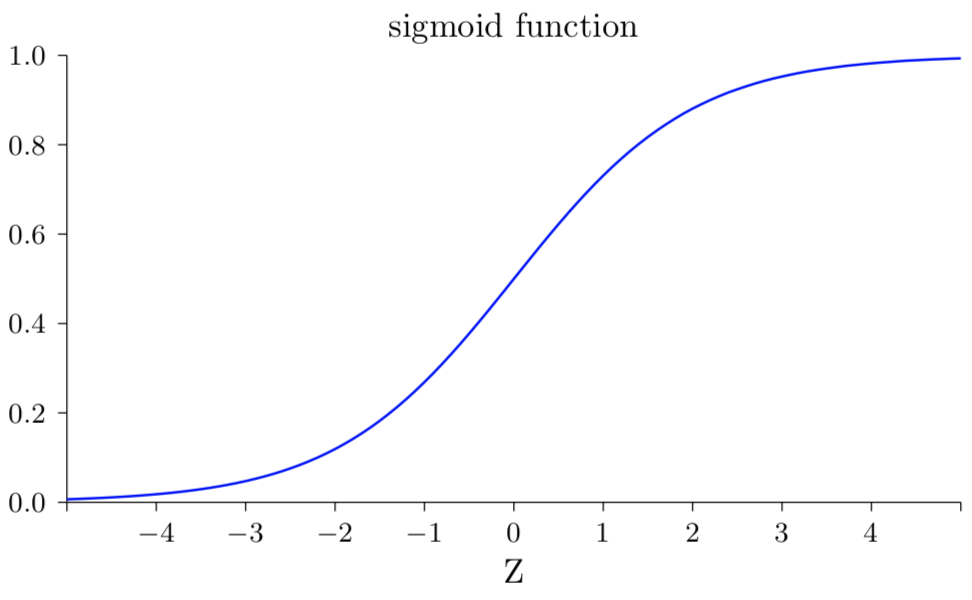
对于上面的sigmoid函数表达式,设置一个具有输入x、权重w和偏置b的S型神经元的输出为:
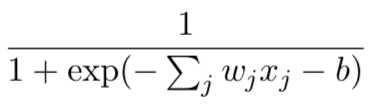
对于上述输出中的e^-z来说:
当z=w·x+b是一个很大的正数时,该输出趋近于1;
当z=w·x+b是一个很大的负数时,该输出趋近于0;
只有在z取中间的一些值的时候,这个S型神经元和感知器才有较大的出入。
如果σ是个阶跃函数,既然输出会依赖于w 4+ 6是正数还是负数2,那么S型神经元会成为一个感知器。所以σ函数的平滑特性,是重点中的重点:σ的平滑意呋着杈重和偏置的微小变化,即∆w和∆σ,会从神经元产生一个微小的输出变化∆output。
神经网络的架构
有了学习算法之后,我们如何搭建一个神经网络?
看看下面的网络架构:
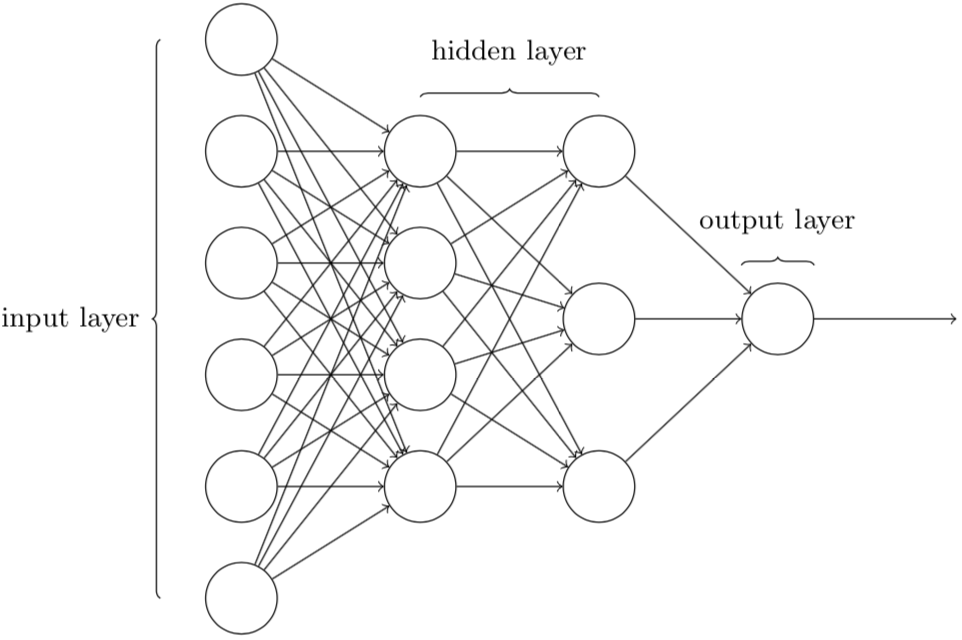
做如下定义:
- 最右边的一列称作输出层(output layer)
- 最左边的一列称作输入层(input layer)
- 所有不是最左边也不是最右边的神经列称作隐藏层(hidden layer)
设计网络的输入输出层通常是比较直接的。例如,假设我们尝试确定一张手写数字的图像上 是否写的是“9”。那么我们可以将图片像素的强度进行编码作为输入神经元来设计网络。 如果图像是一个64 x 64的灰度图像,那么我们会需要4096 = 64 x 64个输入神经元,每个强度 取0和1之间合适的值。输出层只需要包含一个神经元,当输出值小于0.5时表示“输入图像不 是一个9”,大于0.5的值表不“输入图像是一个9”。
而对于隐藏层来说,其设计流程是非常复杂的,也是神经网络架构设计中最重要的部分。目前已有众多的最优法则来帮助我们完成这件事情,让我们所设计的网络的行为更加接近我们内心所想。
一个简单的分类手写数字的网络
根据上面的理论,构造一个简单的分类手写数字的网络!
首先,一个需要说明的问题是,这里的分类网路针对的问题仅仅是识别问题,而图像分割问题则不在考虑范围之内。实际上,只要有足够精准的识别算法,分割问题便不难解决。
我们设想使用一个三层的神经网络来识别单个数字:
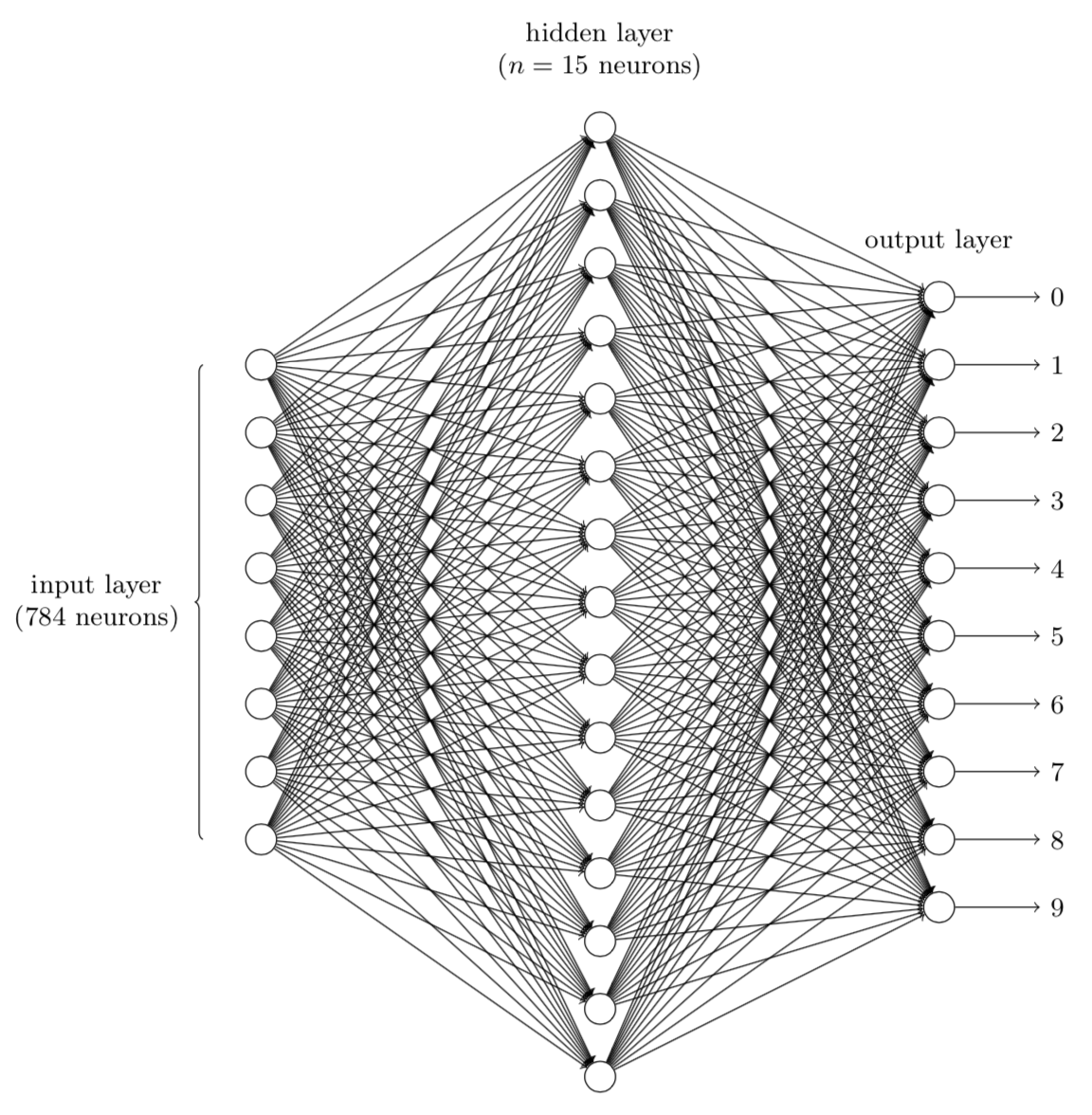
对上面的神经网络做出解释:
网络的输入层包含绐输入像素的值进行编码的神经元:因为绐网络的训练数据会有很多扫描得到的28x28的手写数字的图像组成,所有输入层包含有784=28x28个神经元。为了简化,上图中已经忽略了784中大部分的输入神经元。输入像素是灰度级的,值为0.0表示白色,值为1.0表示黑色,中间数值表示逐渐暗淡的灰色。
网络的第二层是一个隐藏层。我们用n来表示神经元的数量,我们将绐n实验不同的数值。示例中用一个小的隐藏层来说明,仅仅包含n=15个神经元。
网络的输出层包含有10个神经元。如果第一个神经元激活,即输出1,那么表明网络认为 数字是一个0。如果第二个神经元激活,就表明网络认为数字是一个1。依此类推。即此处把输出神经元的输出赋予编号0到9,并计算出那个神经元有最高的激活值。
接下来的这个问题非常重要,它将帮助我们理解隐藏层在干什么:有人可能会好奇为什么用10个输出神经元。毕竟我们的任务是能让神经网络告诉我们哪个数字(0,1,2,…,9)能和输入图片匹配。一个看起来更自然的方式就是使用4个输出神经元,把每一个当做一个二进制值,结果取决于它的输出更靠近0还是1。四个神经元足够编码这个问题了,因为2^3=8 < 10 <2^4=16 。所以为什么我们反而要用10个神经元呢?这样做难道效率不低吗?
对于这个问题,大家的第一反应就是:10个输出神经元的神经网络比4个的识别效果更好。那么接下来的问题是:为什么使用10个输出神经元的神经网络更有效呢。有没有什么启发性的方法能提前告诉我 们用10个输出编码比使用4个输出编码更有好呢?
假设我们用到的这10个输出编码,假设它们之中的每一个的作用是识别图片的一部分(这个假设在这个情景中极其重要!但是在这个情景之外就不重要了)。如果我们识别0的过程如下:

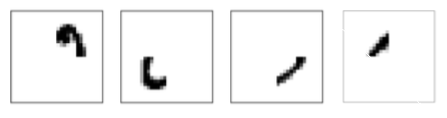
在上面的识别过程中,如果所有隐藏层的这四个神经元被激活那么我们就可以推断出这个数字是0。当然,这不是推断出0的唯一方式,还能通过很多其他合理的方式得到0(通过上述图像的转换,或者稍微变形)。但至少在这个例子中我们可以推断出输入的数字是0。
假设神经网络以上述方式运行,则可以绐出一个合理的理由去解释为什么用10个输出而不是4个:如果我们有4个输出,那么第一个输出神经元将会尽力去判断数字的最高有效位是什么。把数字的最高有效位和数字的形状联系起来并不是一个简单的问题。
上面只是一个启发性的方法。没有什么理由表明这个三层的神经网络必须按照上面描述的方式运行,即隐藏层是用来探测数字的组成形状。可能一个聪明的学习算法将会找到一些合适的权重能让我们仅仅用4个输出神经元就行。但这个启发性的方法是很有效的,我们可以通过这种方法去构建我们想要的神经网路并使它尽可能达到高效。
