原创文章,转载、引用请注明出处!
概述
图像超分辨率,Image Super Resolution(SR);
概念:SR是指通过软件或硬件的方法,从观测到的低分辨率(low resolution)图像重建出相应的高分辨率(high resolution)图像;
更直白的表述为:提高图像的分辨率,使被观察图像给出更清晰的图像表述。
图像超分辨率重建关注的是恢复图像中丢失的细节,即高频信息。在大量的电子图像应用领域,人们经常期望得到高分辨率(简称HR)图像。但由于设备、传感器等原因,我们得到的图像往往是低分辨率图像(LR)。增加空间分辨率最直接的解决方法就是通过传感器制造技术减少像素尺寸(例如增加每单元面积的像素数量);另外一个增加空间分辨率的方法是增加芯片的尺寸,从而增加图像的容量。因为很难提高大容量的偶合转换率,所以这种方法一般不认为是有效的,因此,引出了图像超分辨率技术。
图像分辨率:指图像中存储的信息量,是每英寸图像内有多少个像素点,分辨率的单位为PPI(Pixels Per Inch),通常叫做像素每英寸。一般情况下,图像分辨率越高,图像中包含的细节就越多,信息量也越大。图像分辨率分为空间分辨率和时间分辨率。通常,分辨率被表示成每一个方向上的像素数量,例如64*64的二维图像。但分辨率的高低其实并不等同于像素数量的多少,例如一个通过插值放大了5倍的图像并不表示它包含的细节增加了多少。
应用:在监控设备、卫星图像遥感、数字高清、显微成像、视频编码通信、视频复原和医学影像等领域都有重要的应用价值。
分类:SR的应用方向大致可分为两种。一是Image SR。只参考当前低分辨率图像,不依赖其他相关图像,称之为单幅图像的超分辨率(single image super resolution,SISR)。Image SR的方法多种多样,从最基础的插值到现如今的深度学习,是一个非常热门的研究方向。另一是Video SR。参考多幅图像或多个视频帧的超分辨率技术,称之为多帧视频/多图的超分辨率(multi-frame super resolution)。
传统的Image SR技术
基于插值的Image SR
何为“插值”?
通过某个点周围若干个已知点的值,以及周围点和此点的位置关系,根据一定的公式,算出此点的值,就是插值法。
例如,有如下2*2的图像,不同颜色代表不同的像素点值:

使用插值算法给上面的这张图像做细节扩充,形成一张4*4大小的图像:

由于已经得知原2*2图像中的4个像素点的值,那么在接下来的操作中,仅需要求剩余12个点(黑色)的值即可。通过某个点周围若干个已知点的值,以及周围点和此点的位置关系,根据一定的公式,算出此点的值,就是插值法。如何把原图像的点摆放在新图中(确定具体坐标);未知的点计算时,需要周围多少个点参与,公式如何。对于上面的问题,不同的方案选择,就是不同的插值算法。
常用的插值算法有:最邻近元法,双线性内插法,双三次内插法等。
实际上,这类插值算法,提升的图像细节有限,所以使用较少。通常,通过多幅图像之间的插值算法来重建是一个手段。
以2*2为例。放大2倍后,得到一个4*4的图片。其中(0,0)的灰度值与之前的(0,0)相同。(2,0) 与之前的 (1,0)的灰度值相同。那么,这个放大图像的 (1,0)的灰度值等于什么呢?等于原图像的(1/2,0)的灰度值。但是原图像并没有这个点,通过以下插值方法,可计算该点的像素值灰度。
最邻近插值
这是最简单的插值算法。思路是:当图片放大时,缺少的像素通过直接使用与之最近原有颜色生成。
可理解为“按比例放大”:放大之后缺少的内容,直接照搬最近的已知的内容。
首先要确定:原图像的像素摆放在新图中的具体坐标。新坐标对应源图中的坐标可以由如下公式得出:
1 | srcX = dstX * ( srcWidth / dstWidth ) |
这里依旧可以用“按比例放大”来理解:将srcWidth / dstWidth称为缩放系数K。
坐标必然是整数,但是上述公式不一定会得到整数(K不一定为整数)。当2*2放大到4*4,结果和2.2.1中相同。但如果将2*2放大到3*3,就会出现新的像素点坐标计算出来有小数点的情况。这里需要采用的策略是四舍五入的方法(也可直接舍掉小数位),把非整数坐标转换成整数。
接下来,以图片的左上角建立坐标,并将待求象素的四已知邻象素中左上角的看作[i,j],则待求像素的值依赖于以下四个已知坐标:[i,j]、[i,j+1]、[i+1,j]、[i+1,j+1],对于每一个待求象素,将距离待求象素最近的邻灰度赋给待求象素。
当待求像素距离四个已知邻象素的距离中的两个及以上都是最小时,给定一个统一的规则即可,例如:要么都取原坐标中的小值,要么都取大值等。
图像右侧和下侧的待求像素并不像图像中部的像素,拥有四个已知邻象素。它们最多拥有1个(图像右下角的区域)或2个邻象素,规则也是同样的。
对于上面的2*2图像,扩大到3*3和4*4时,将得到:

由于2*2实在是太小,下面的两种插值法的到的3*3和4*4实际上和上面这个结果是一致的。
最邻近插值有着明显的缺陷,它会使结果图像产生明显可见的锯齿。
双线性插值
在数学上,双线性插值是有两个变量的插值函数的线形插值扩展,其核心思想是在两个方向分别进行一次线性插值。
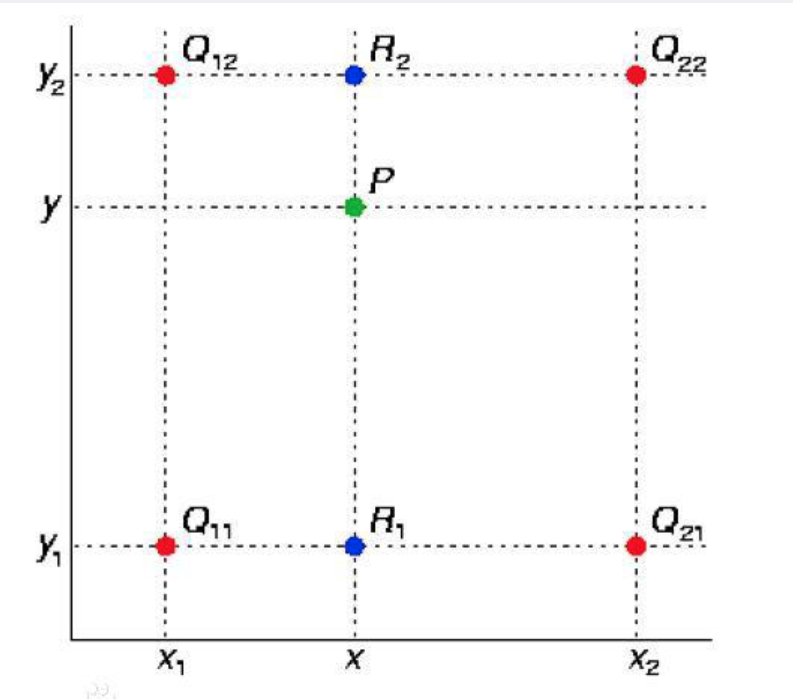
假设已知上图中已知红色数据点的值,要求是通过双线性插值得到绿色数据点的值。将需求描述为数学方式:预得到未知函数f在点P(x,y)的值,并假设已知函数f有Q11、Q12、Q21、Q22四个坐标。
首先在x方向进行线性插值,得到:
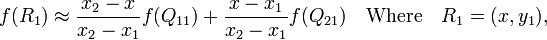
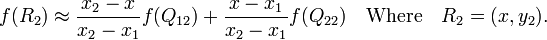
然后在y方向进行线性插值,得到:
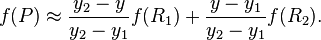
那么未知函数f就可以描述如下:
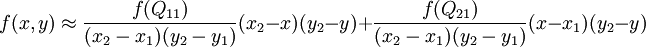
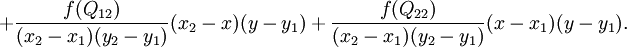
如果选择一个坐标系统使得f的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为:
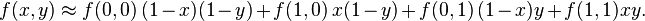
用矩阵运算表示为:
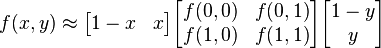
双线性内插法的结果通常不是线性的,线性插值的结果与插值的顺序无关。双线性内插法的计算比最邻近点法复杂,计算量较大但,没有灰度不连续的缺点。具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
先进行y方向的插值,然后进行x方向的插值,所得到的结果同先x后y是一致的。
相对于最近邻插值简单的四舍五入,双线性插值的处理更为科学,优化了边缘保护。
双三次内插法
Cubic Convolution Interpolation for Digtial Image Processing
双三次插值(bicubic)又称双立方插值。
在数值分析这个数学分支中,双三次插值是二维空间中最常用的插值方法。在这种方法中,函数f在点(x,y)的值可以通过矩形网格中最近的十六个采样点的加权平均得到,在这里需要使用两个多项式插值三次函数,每个方向使用一个。
双三次插值的本质就是用使用了两次Cubic Interpolation。
Cubic Interpolation
f(0)、f(1)已知
假设已知f(0),f(1)以及其导数一共四个值。用Cubic Interpolation计算f(0.5)的值。
假设:
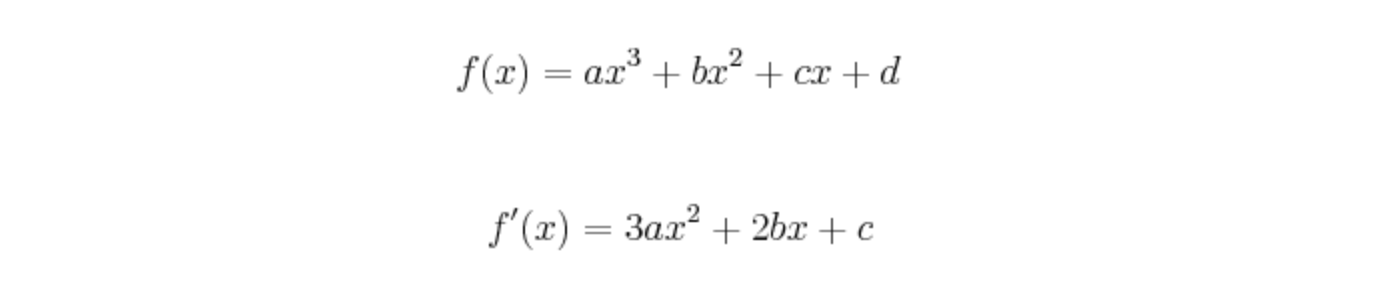
因为已知f(0)、f(1)以及其导数四个值:
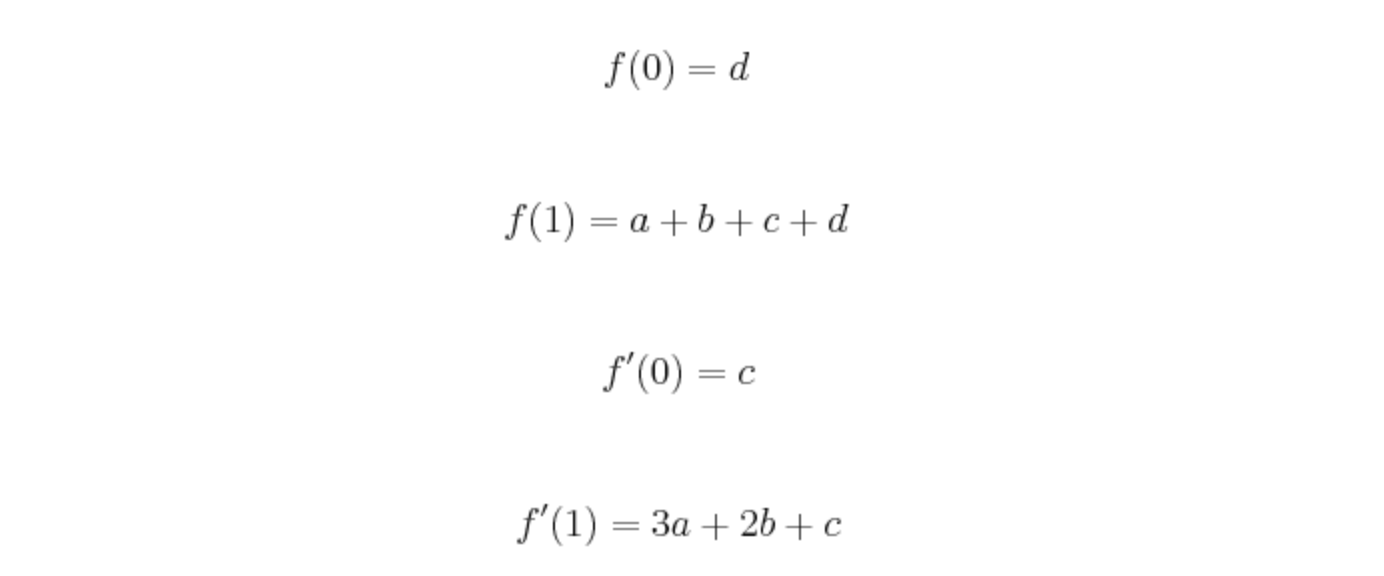
可得:
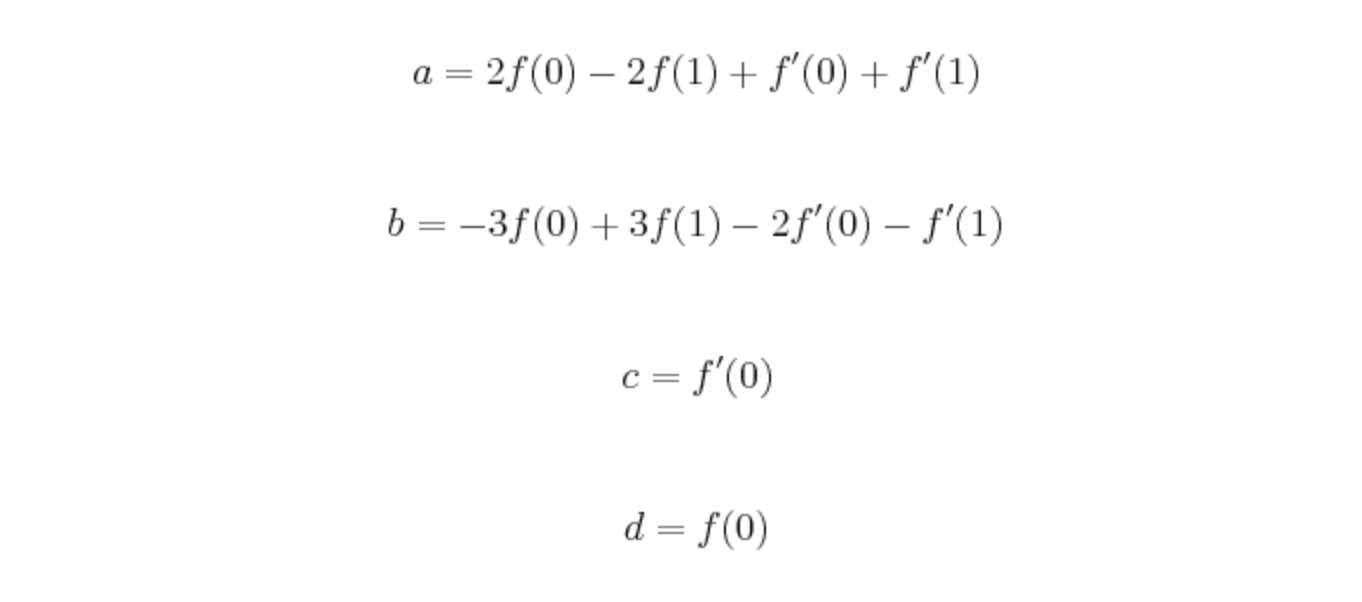
通过解出上述四个代数,可以算出f(0.5)。
f(0)、f(1)未知
大多数情况下,并不知道f(0)、f(1)的导数。
设f(-1)=P0、f(0)=P1、f(1)=P2、f(2)=P3。有:
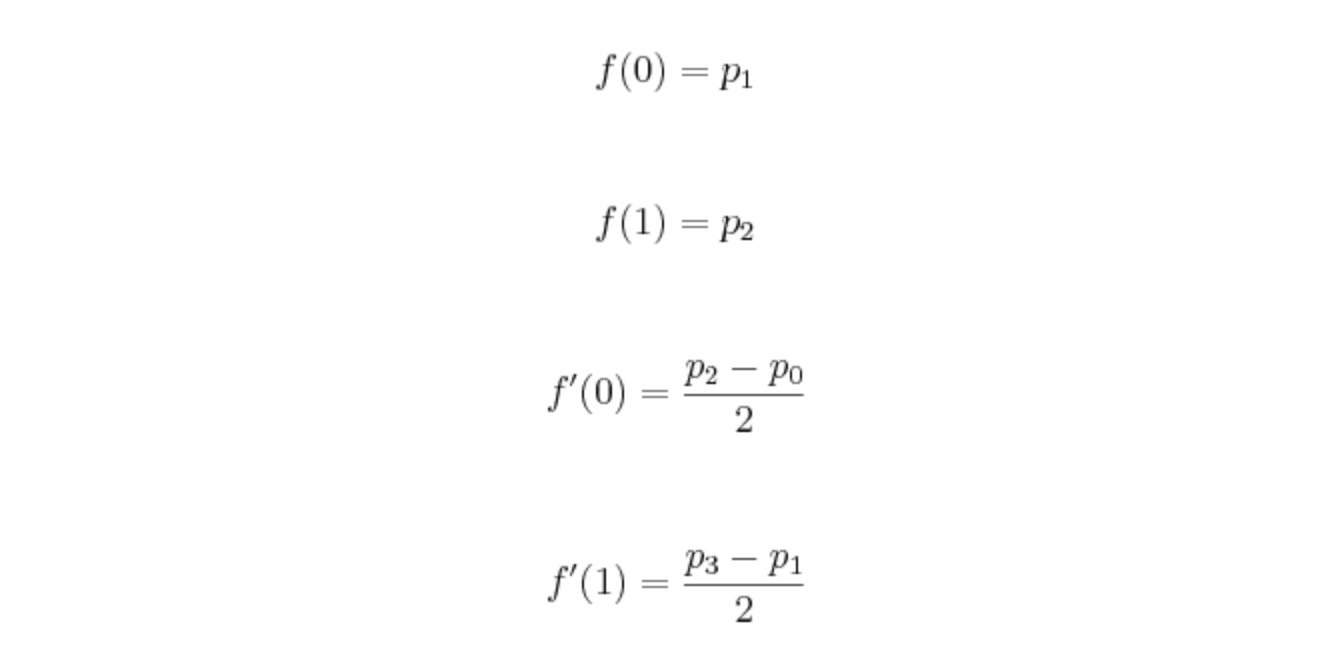
后两值一般使用相邻两个点的斜率代替。但在更多的情况下,并不知道边缘值的斜率(因为边缘点的相邻两个点知道不完全)。所以有如下两个方法去代替:
Left: p0 = p1、Right: p3 = p2
Left: p0 = 2p1 - p2、Right: p3 = 2p2 - p1
两次Cubic Interpolation
原来的一次导数,变成了偏导。
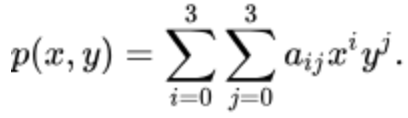
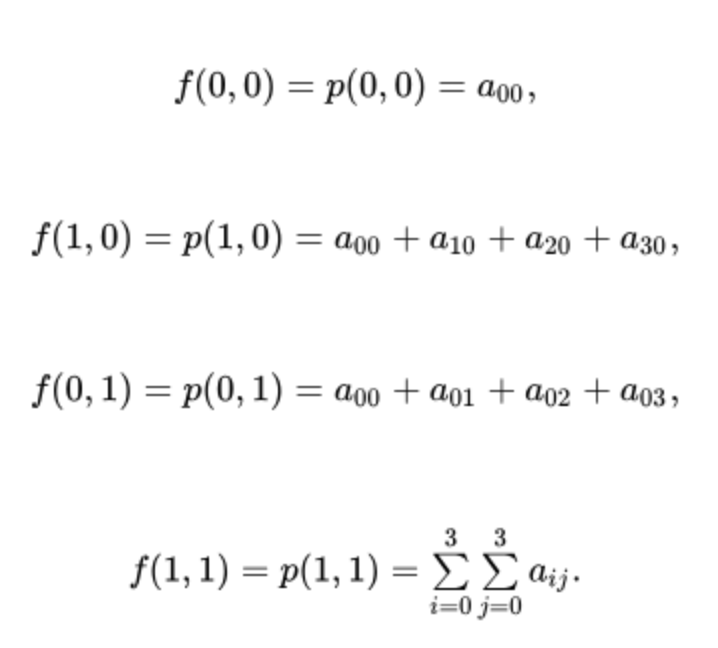
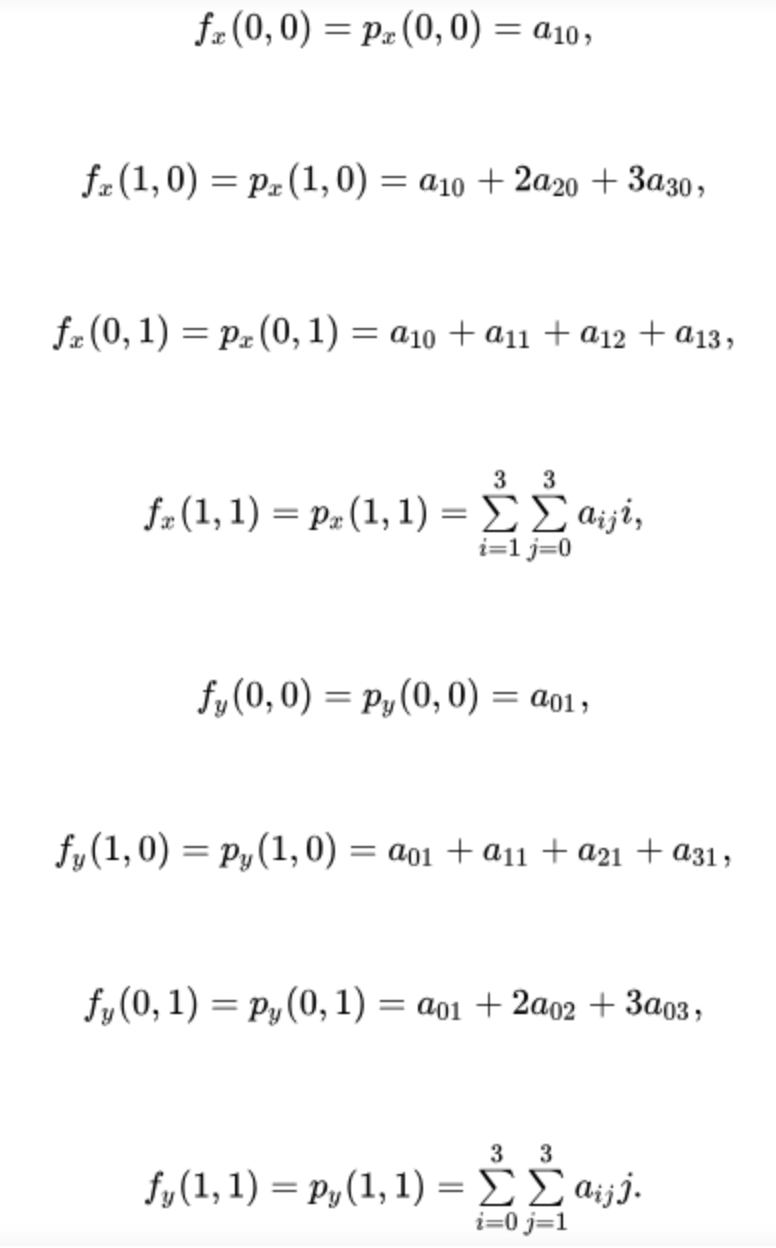
这四个点的灰度值必然满足第一个方程。通过上述三组方程,求出所有未知数。从而计算f(0.5,0)。
插值法的总结
对于上述三种不同的插值技术:
特性:最邻近插值,名称非常直白,核心是四舍五入选取最接近的整数。这样的做法就会导致像素的变化不连续,在图像中的体现就是会有锯齿。双线性插值则是利用与坐标轴平行的两条直线去把小数坐标分解到相邻的四个整数坐标点的和。双三次插值与双线性插值类似,只不过用了相邻的16个点。
坐标权重:前两种方法能回保证两个方向的坐标权重和为1,但是双三次插值不能保证这点,所以又可能去出现像素值越界的情况,需要截断。
效果与泛用性:双三次插值通常能产生效果最好、最精确的插补图形,但它速度也是最慢的。双线性插值的速度则要快一些,但没有前者精确。在商业性图像编辑软件中,经常采用的是速度最快,但也是最不准确的最近相邻插值。
基于重建的Image SR
何为“重建”?
基于重建的SR,其基础是均衡及非均衡采样定理。这类算法的思路大多都是通过多帧低分辨率的图像恢复出一幅高分辨率图像,利用低分辨率图像中的丰富信息来进行超分辨处理,从而获得比观测图像分辨率更高的图像,即它假设低分辨率的输入采样信号(图像)能很好地预估出原始的高分辨率信号(图像)。绝大多数超分辨率算法都属于这一类,进一步的分类则有频域法和空域法。
Nyquist-Shannon采样定理:如果希望得到的采样型号有旋转和相位变化,那么采样周期要小于整数周期的1/2,采样频率应该大于原始频率的2倍。同理,对于模拟信号,如果希望得到信号的各种特性,采样频率应该大于原始模拟信号的最大频率的两倍,否则将发生混叠(相位/频率模糊)。
在统计、信号处理和相关领域中,混叠是指取样信号被还原成连续信号时产生彼此交叠而失真的现象。当混叠发生时,原始信号无法从取样信号还原。而混叠可能发生在时域上,称做时间混叠,或是发生在频域上,被称作空间混叠。
频率域方法
频率域方法是图像超分辨率重建中一类重要方法,其中最主要的是消混叠重建方法。
消混叠重建方法是通过解混叠而改善图像的空间分辨率实现超分辨率复原。在原始场景信号带宽有限的假设下,利用离散傅立叶变换和连续傅立叶变换之间的平移、混叠性质,给出了一个由一系列欠采样观察图像数据复原高分辨率图像的公式。多幅观察图像经混频而得到的离散傅立叶变换系数与未知场景的连续傅立叶变换系数以方程组的形式联系起来,方程组的解就是原始图像的频率域系数,再对频率域系数进行傅立叶逆变换就可以实现原始图像的准确复原。
空间域方法
在空间域方法中,其线性空域观测模型涉及全局和局部运动、光学模糊、帧内运动模糊、空间可变点扩散函数、非理想采样等内容。空域方法具有很强的包含空域先验约束的能力,主要包括非均匀空间样本内插、迭代反投影方法(IBP)、凸集投影法(POCS)、最大后验概率、最优和自适应滤波方法、确定性重建方法等。
非均匀空间样本内插
非均匀空域样本内插法是最直观的超分辨率图像重建算法,一般包含三个基本步骤:(1)运动估计;(2)非线性内插得到高分辨率图像;(3)解除混叠。非均匀空间样本内插法首先对低分辨率视频序列进行运动补偿,继而采用内插的方法产生分辨率较高的合成图像,以这个合成图像中作为初始值,再用Landweber迭代法重建超分辨率图像,最后对超分辨率图像进行去模糊操作。
非均匀空间样本内插方法运算量较低,能适用于实时任务;但过于简单化,在重建时不能得到比低分辨率图像中更多地频率成分,退化模型受限制,只适用于模糊和嗓声特性对全部低分辨率图像都一样的情况,也没有使用先验约束。
凸集投影法(POCS)
凸集投影算法是把未知图像假设为一个适宜的希尔伯特空间中的元素,关于未知图像的每一个先验知识或约束限制了希尔伯特空间中的一个封闭凸集的解,引入幅度边界的限制,导出求解未知图像的迭代公式,由初始估计迭代计算超分辨率图像。利用集合论方法来恢复超分辨率图像,它有效地利用了空间范围观察模型,同时允许包含先验信息。
综上,POCS算法是一个迭代过程,给定超分辨率图像空间上的任意一个点,来定位一个能满足所有凸集的点。
迭代反投影法(IBP)
顾名思义,该算法也是一个迭代过程。在迭代反投影法中,首先估计一个高分辨率图像作为初始解(通常采用的是单幅低分辨率图像的额差值结果),然后根据系统模型,计算其模拟低分辨率图像(1984年提出时,示例为线型模型)。如果初始解与与原始的高分辨率图像精确相等,并且模拟成像过程符合实际情况,则模拟低分辨率序列应与观察到的实际的低分辨率图像相等。当两者不同时,将它们之间的误差反向投影到初始解上,使其得到修正。当误差满足要求时,结束迭代过程,给出最终结果。
IBP算法直观,计算简单,但是由于没有考虑嗓声的影响,对高频嗓声非常敏感,并且由于逆问题的病态性,该方法没有唯一解,选择系数也有一些难度。与POCS等一些空间域方法相比,IBP算法难以利用空间先验信息。
统计复原类方法
统计复原方法将SR看成是一个统计估计问题。它为求解病态的超分辨率问题加入必要的先验约束,为能得到满意解提供了可能。常用的统计复原方法包括最大后验概率(MAP)估算法和最大似然(ML)估算方法。最大后验概率就是在己知低分辨率序列的前提下,使出现高分辨率图像的后验概率达到最大,最大似然估算方法可认为是最大后验概率先脸模型下的特例。
最大后验概率估计是后验概率分布的众数。利用最大后验概率估计可以获得对实验数据中无法直接观察到的量的点估计。
最大似然估计一种重要而普遍的求估计量的方法。最大似然法明确地使用概率模型,其目标是寻找能够以较高概率产生观察数据的系统发生树。
混合MAP/POCS方法
POCS和MAP是重建类SR算法中效果出众的两种,两者都很容易引入先验知识。其中POCS算法保持图像边缘和细节的能力很强,但收敛稳定性不高,没有唯一解,降嗓能力不强;MAP有唯一解且收效稳定性高,降嗓能力强,但边缘和细节保持能力不如POCS。混合MAP/POCS方法则结合两者的优势特征,得到HR图像的最佳估计。
混合MAP/POCS方法有效结合了全部先验知识,并且能确保唯一的最优解,是一种重建效果较好的算法。
滤波类方法
IBP、POCS、MAP、MAP/POCS等几种超分辨率算法的运算量大,只能应用于实时性要求不高的图像SR情况,如遥感图像和医学图像的超分辨率处理。在实时性要求比较高的情况下,例如实时视频的超分辨率复原,要求算法既能提高图像的分辨率,运算复杂度又比较低。滤波的方法,如自适应滤波、Wiener滤波和Kalman滤波等方法运算复杂度低,适用于对运算速度要求比较高的场合。
基于学习的Image SR
在超分辨率重建的过程中,随着要求分辨率倍数的增加,低分辨率图像序列的冗余信息已经不能提供满足要求的高频细节。通过增加低分辨率图像序列帧数的方法得到的高频信息也是不能满足实际要求的。在这种情况下,利用神经网络的方法,通过学习训练来获得图像的先验信息,可以得到包含更多细节的高分辨率图像。
从理论上讲,如果训练集合是通用的,就可以利用这个训练集合对各种类型的图像进行放大。
机器学习领域(非深度学习邻域)的一些主流的Image SR方法如下:
Example-based方法
邻域嵌入方法
支持向量回归方法
虚幻脸
很多人脸图像是被现场照相机获取的,由于环境限制或设备原因,这些图像经常存在分辨率较低的问题。在人脸分析识别领域,怎样恢复人脸图像已经成为一个重要的课题。这个问题在Baker和Kanade的先驱工作中第一次被定义为虚幻脸。
- 稀疏表示法
基于深度学习的Image SR技术
基于深度学习的图像超分辨率重建的大值研究流程如下:
给出初始图像输入Image_1;
然后将初始图像输入进行分辨率的降低,称为Image_2;
通过各种深度学习算法,将Image2重建为Image3,且Image3和Image1的分辨率一致(SR的工作部分),再由PSNR等方法比较Image1与Image3,验证SR重建的效果,并根据效果调节神经网络中的节点模型和参数;
迭代第三步直到得到满意的结果。
接下来给出近年来较为有代表性的基于深度学习的Image SR方法:
发展历程:SRCNN -> FSRCNN -> ESPCN -> VDSR -> SRGAN -> ESRGAN -> EDSR
额外的一篇:PULSE
SRCNN
见《论文研读:SRCNN》。
FSRCNN
Accelerating the Super-Resolution Convolutional Neural Networks
这篇文章指出,SRCNN在速度方面有着显著的限制。体现在:
低分辨率图像需要上采样(双三次插值);
非线性映射步骤,参数量依旧影响速度。
这篇文章主要的目的是对SRCNN进行加速。文章重新设计SRCNN结构,体现在以下三个方面:
在网络的最后新增添了一个解卷积层,作用是从没有插值的低分辨率图像直接映射到高分辨率图像;
重新改变输入特征维数;
使用了更小的卷积核但是使用了更多的映射层。
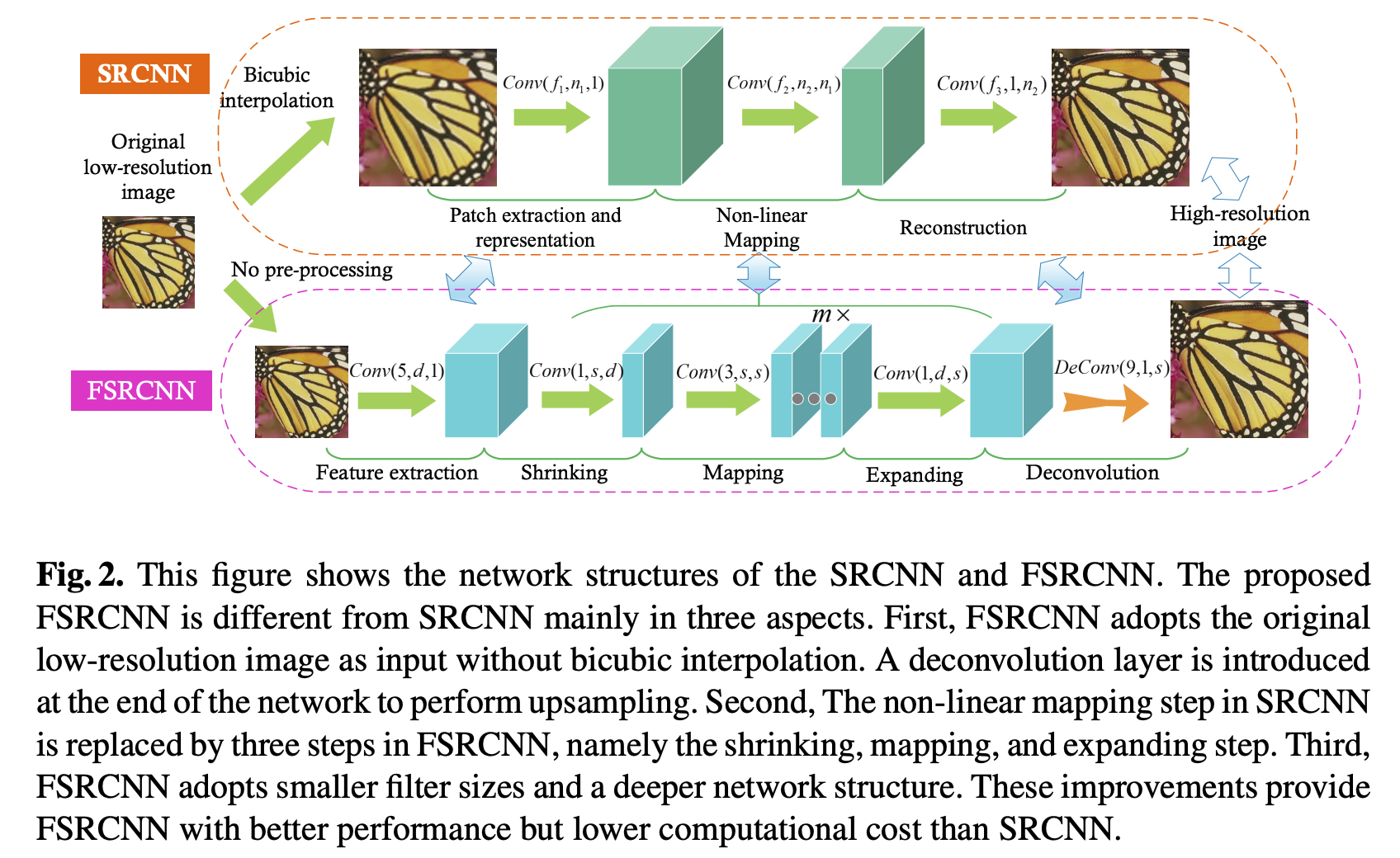
对于上述第一个问题,采用解卷积层代替三次插值,针对第二个问题,添加萎缩层和扩张层,并将中间那一个大层用一些小层(卷积核大小是3*3)来代替。整个网络结构类似于漏斗的形状,中间细两端粗。这个网络不仅仅速度快,而且不需要更改参数(除新增添的在最后的解卷积层)。
损失函数:同SRCNN一致的MSE。
Cost function: Following SRCNN, we adopt the mean square error (MSE) as the cost function.
激活函数:改成了PReLU。
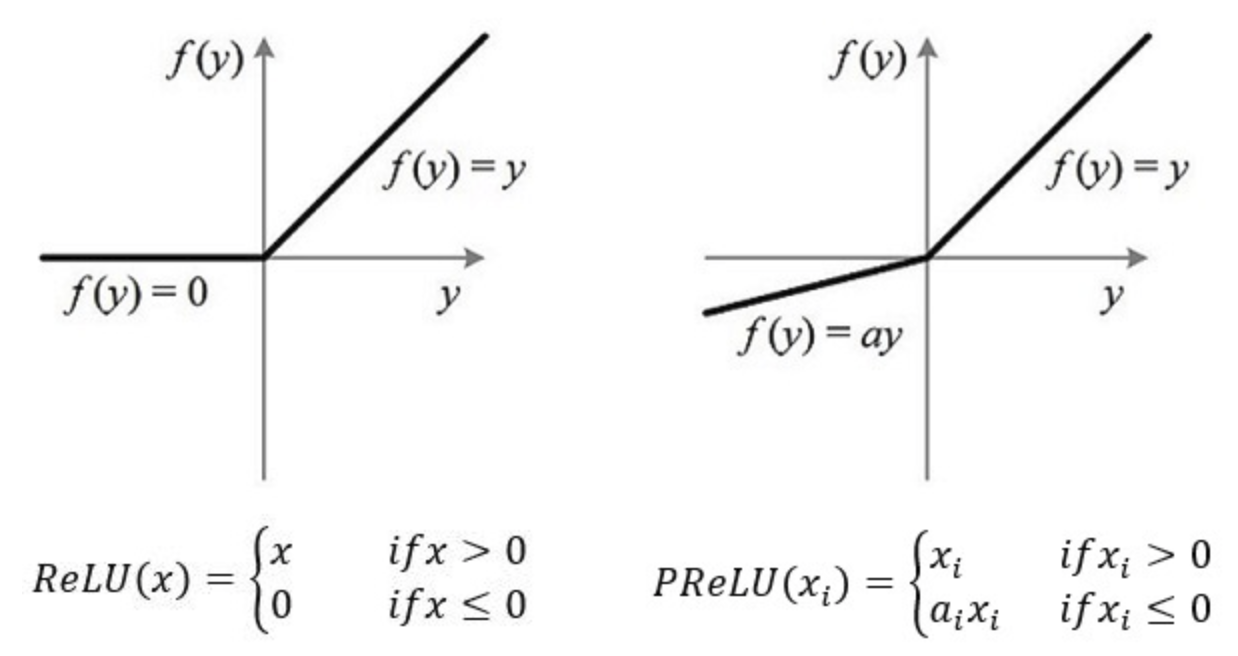
PReLU(Parametric Rectified Linear Unit),带参数的ReLU。i表示不同的通道,如果ai=0,那么PReLU退化为ReLU;如果ai是一个很小的固定值(如ai=0.01),则PReLU退化为Leaky ReLU(LReLU)。有实验证明,与ReLU相比,LReLU对最终的结果几乎没什么影响。
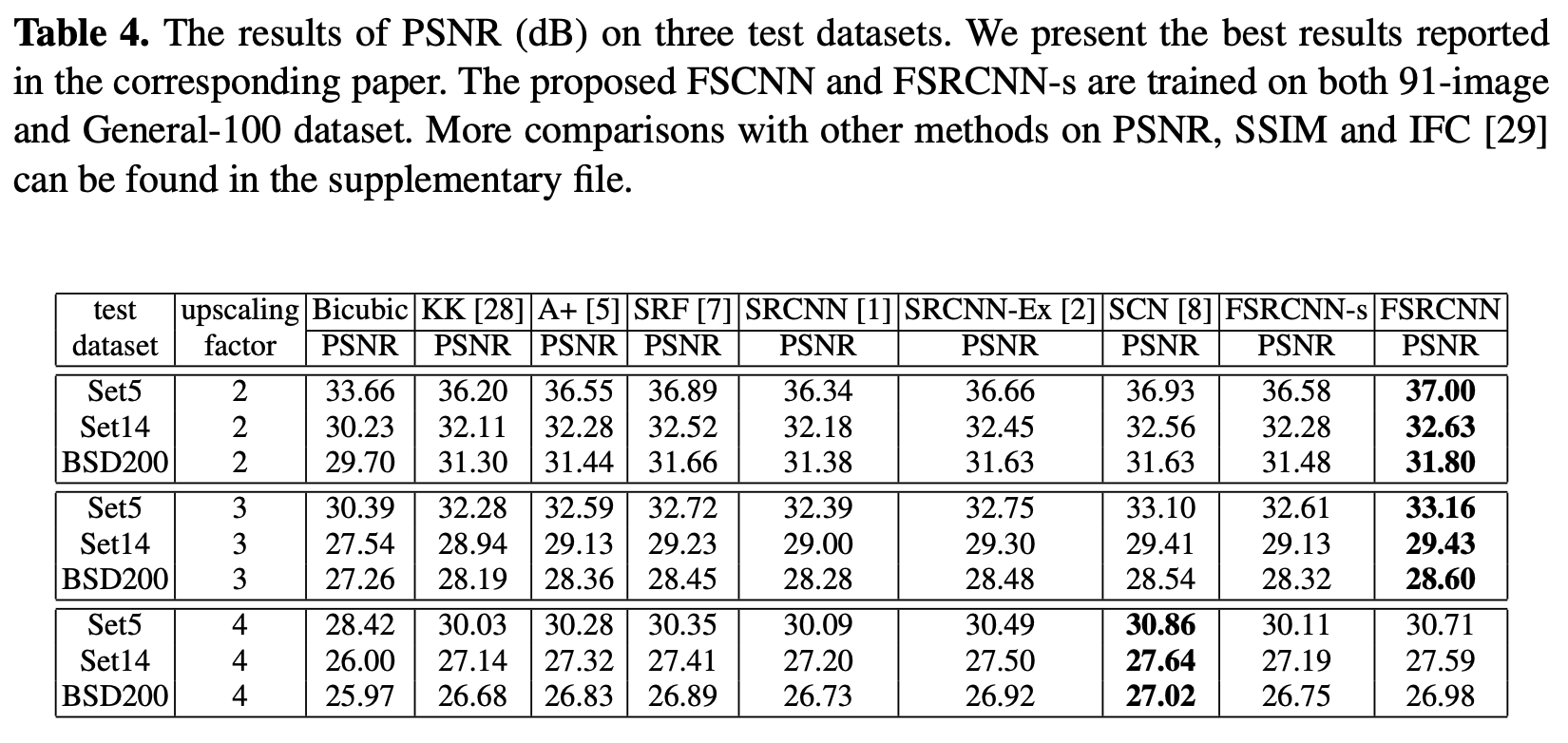
实验结果:
不同倍数、不同数据集、不同方法的对比:在SET5上的结果最好,放大2、3倍时的效果最好。
经典的lenna的结果,SET14在3倍下的模型。

三个贡献:
设计漏斗结构的卷积网络,不需要预处理操作;
速度提升;
训练速度快。
链接:https://arxiv.org/pdf/1608.00367v1.pdf
代码:https://github.com/yifanw90/FSRCNN-TensorFlow
ESPCN
Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network
这篇文章指出,像SRCNN这一类的方法,需要将低分辨率图像通过上采样插值得到与高分辨率图像相同大小的尺寸,再输入到网络中,这意味着要在较高的分辨率上进行卷积操作,从而增加了计算复杂度。
然后这篇文章给出了一种直接在低分辨率图像尺寸上提取特征,计算得到高分辨率图像的高效方法,称为ESPCN。网络结构如下所示:
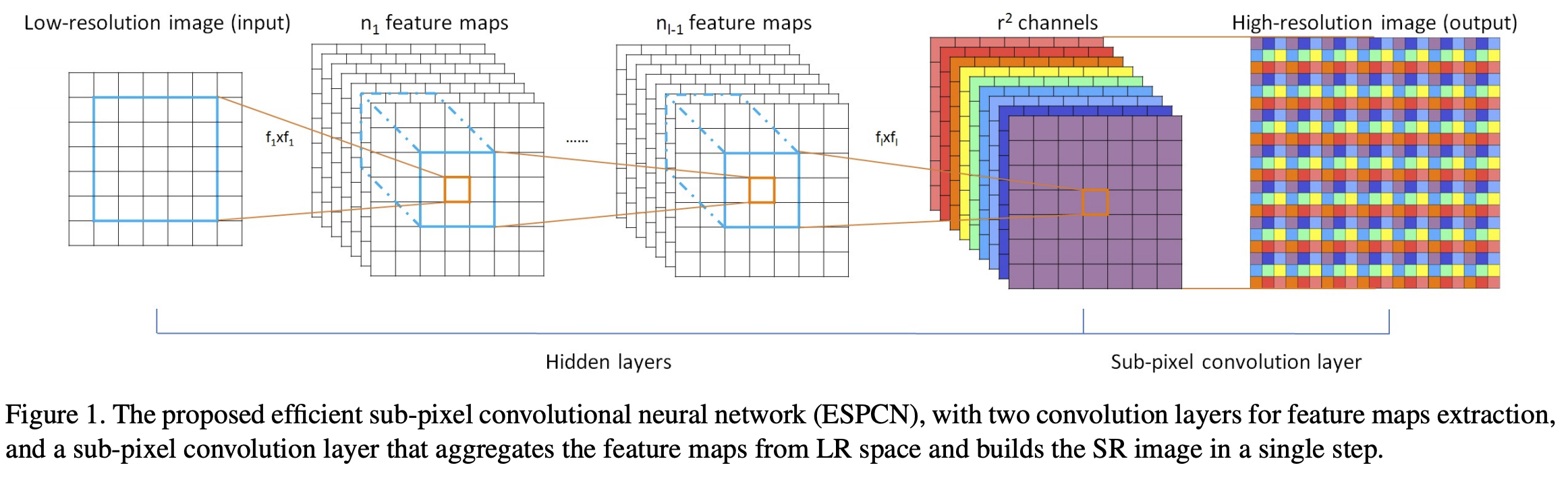
最大贡献:亚像素卷积层/子像素卷积层/pixel shuffle
SR的流程里需要将一张低分辨率图像转换成一张高分辨率图像。如果直接用deconvolution作为upscale手段的话,通常会带入过多人工因素进来(有不少论文提到这个)。在反卷积里会存在大量补0的区域,这可能对结果有害。因此pixel shuffle通过亚像素卷积,实现从低分辨图到高分辨图的重构,通过将多通道feature上的单个像素组合成一个feature上的单位即可,每个feature上的像素就相当于新的feature上的亚像素。
所以在图像超分辨的任务多使用pixel shuffle的方式获得高分辨图像(ESPCN等很多论文都有)。
亚像素:在相机成像的过程中,获得的图像数据是将图像进行了离散化的处理,由于感光元件本身的能力限制,到成像面上每个像素只代表附近的颜色。例如两个感官原件上的像素之间有4.5um的间距,宏观上它们是连在一起的,微观上它们之间还有无数微小的东西存在,这些存在于两个实际物理像素之间的像素,就被称为“亚像素”。亚像素实际上应该是存在的,只是缺少更小的传感器将其检测出来而已,因此只能在软件上将其近似计算出来。
若输出是原来的 r * r 倍(如,r=2,200x200 变成 400x400),则输出的 channel 数是输入 channel 数除以 r * r (如200x200x40 变成 400x400x10)。
一文搞懂 deconvolution、transposed convolution、sub-pixel or fractional convolution:https://www.cnblogs.com/shine-lee/p/11559825.html#convolution过程
链接:https://arxiv.org/pdf/1609.05158.pdf
code:https://github.com/JuheonYi/VESPCN-tensorflow
VDSR
Accurate Image Super-Resolution Using Very Deep Convolutional Networks
本文提出,输入的低分辨率图像和输出的高分辨率图像在很大程度上是相似的,也就是指低分辨率图像携带的低频信息与高分辨率图像的低频信息相近,训练时带上这部分会多花费大量的时间,实际上只需要学习高分辨率图像和低分辨率图像之间的高频部分残差即可。残差网络结构的思想特别适合以这个思路来解决SR问题,可以说影响了之后的深度学习超分辨率方法。
对SRCNN收敛速度的分析有点牵强,主要是提出了论文的基于残差建模。
何恺明在2015年的时候提出了残差网络ResNet。ResNet的提出,解决了之前网络结构比较深时无法训练的问题,性能也得到了提升,ResNet也获得了CVPR2016的best paper。残差网络结构(residual network)被应用在了大量的工作中。
这篇文章依旧以SRCNN开启叙述,先提了SRCNN的优势,然后指出了SRCNN的三个缺点:
依赖小图像区域的上下文;
收敛太慢;
只能做单个倍数的采样。
first, it relies on the context of small image regions; second, training converges too slowly; third, the network only works for a single scale
然后针对上面三个问题来概括本篇创新点:
Context(增大感受野);
Convergence(残差学习和高学习率);
Scale Factor(使用mutil-scale)。
提出如下的VDSR:
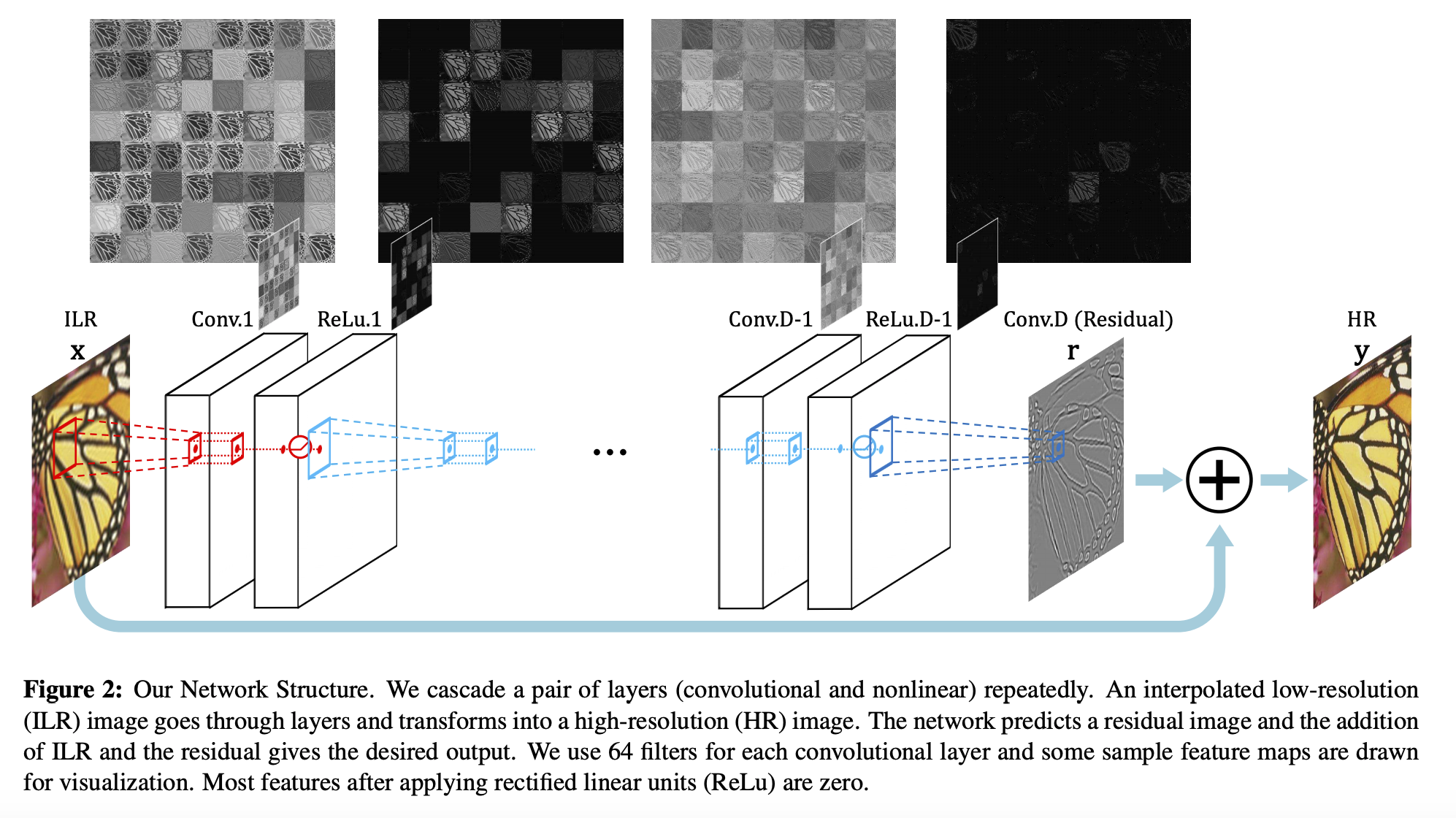
20层的卷积核大小都为3*3*64,
使用插值将LR图片放大到期望的尺寸,再作为网络的输入
每经过一层,feature map将会变小,论文只用补0的方法来保持其尺寸不变。
Loss依旧使用的是MSE:

code:https://github.com/huangzehao/caffe-vdsr 、https://github.com/Jongchan/tensorflow-vdsr 、https://github.com/twtygqyy/pytorch-vdsr
SRGAN
见《论文研读:SRGAN》。
ESRGAN
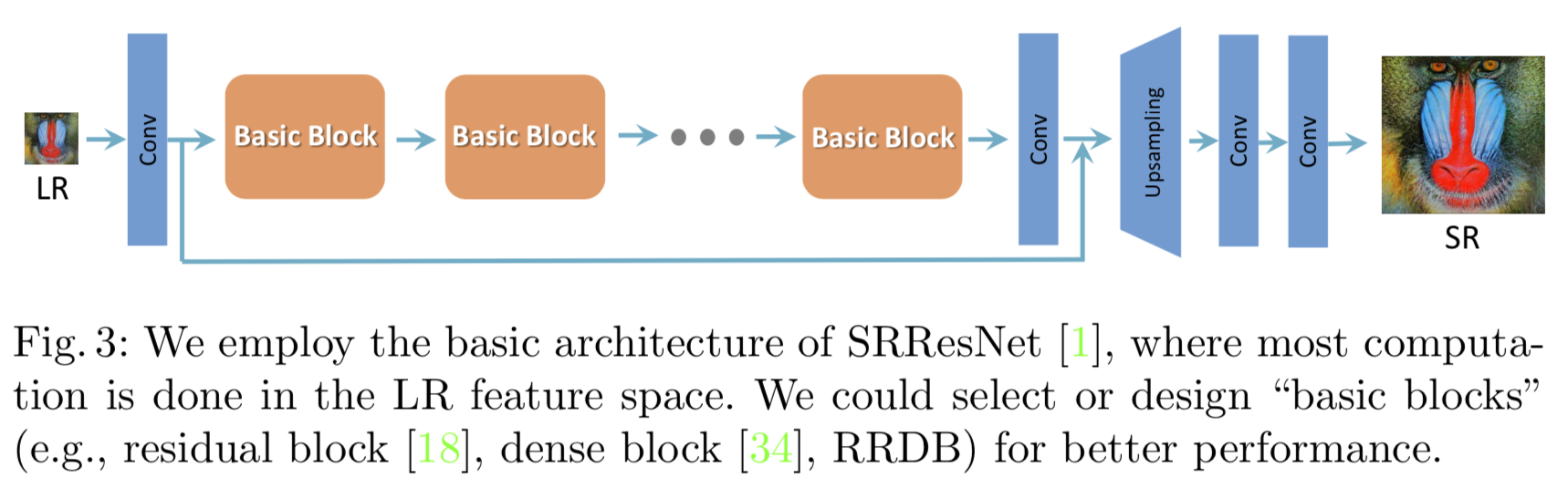
ESRGAN的整体框架和SRGAN保持一致。相比SRGAN,ESRGAN有5处改进:
去除BN层
为什么要去除BN层?
How does batch normalization help optimization
对于有些像素级图片生成任务来说,BN效果不佳。对于图片分类等任务,只要能够找出关键特征,就能正确分类,这算是一种粗粒度的任务,在这种情形下通常BN是有积极效果的。但是对于有些输入输出都是图片的像素级别图片生成任务,比如图片风格转换等应用场景,使用BN会带来负面效果,这很可能是因为在Mini-Batch内多张无关的图片之间计算统计量,弱化了单张图片本身特有的一些细节信息。
以图像超分辨率来说,网络输出的图像在色彩、对比度、亮度上要求和输入一致,改变的仅仅是分辨率和一些细节。而BN,对图像来说类似于一种对比度的拉伸,任何图像经过BN后,其色彩的分布都会被归一化。也就是说,它破坏了图像原本的对比度信息,所以BN的加入反而影响了网络输出的质量。ResNet可以用BN,但也仅仅是在残差块当中使用。
用Dense Block替换Residual Block
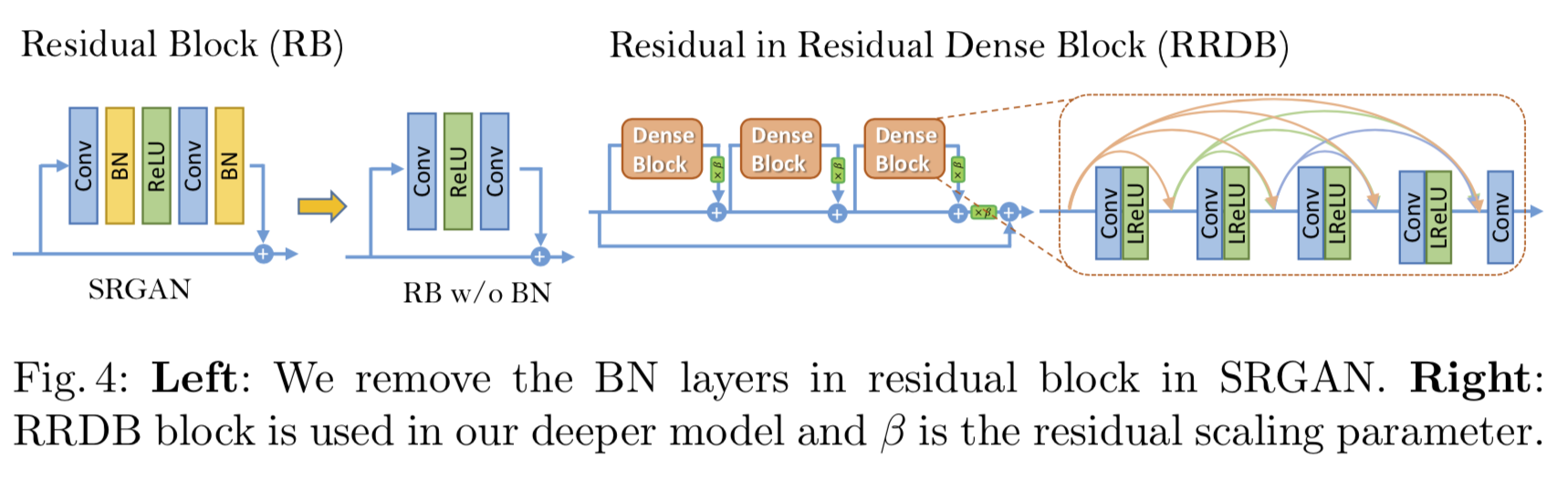
BN的作用是网络更容易优化,不容易陷入局部极小值。ESRGAN去掉了BN,可以猜想,如果保持原有的Residual Block结构,网络会变得非常难易训练,而且很容易陷入局部极小值导致结果不好。
而DenseNet的解空间非常平滑,换言之,DenseNet相比其他网络要容易训练的多,Dense Block和BN提升网络性能的原因是相同的。
总的来说,去掉BN层是因为BN层有副作用,但是BN也有众多的优点且与Dense Block的作用相似,那么用Dense Block替换Residual Block是要弥补去掉BN带来的负面效果。
使用Relativistic GAN改进对抗损失函数
使用relu激活前的特征图计算损失
原文给出的解释如下:
激活后的特征图变的非常稀疏,丢失了很多信息;
使用激活后的特征图会造成重建图片在亮度上的不连续。
生成器的损失函数为:
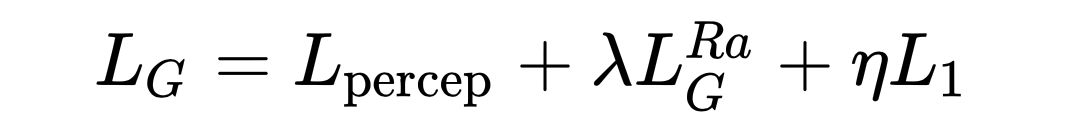
ESRGAN在生成器上的Loss几乎沿用了SRGAN,但是命名是有出入的。
使用network interpolation平衡主客观指标
基于GAN的方法有一个缺点,经常会生成奇怪的纹理,而非GAN的方法总是缺失细节,能不能把两种方法生成的图片加权相加呢?将这样的思路称为Network Interpolation,网络插值。
具体做法是,训练一个非GAN的网络,在这个网络的基础上fine-tuning出GAN的生成器,然后把两个网络的参数加权相加:
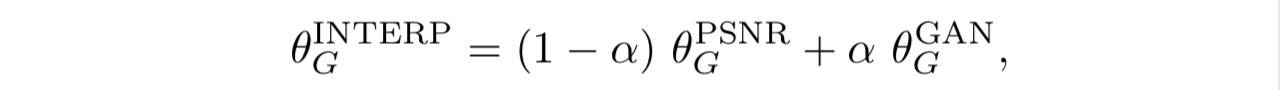
链接:https://arxiv.org/pdf/1809.00219.pdf
code:https://github.com/xinntao/ESRGANgithub.com
EDSR和MDSR
Enhanced Deep Residual Networks for Single Image Super-Resolution
EDSR是NTIRE2017超分辨率挑战赛上获得冠军的方案。
EDSR的最大贡献是去除了SRResNet上的BN。
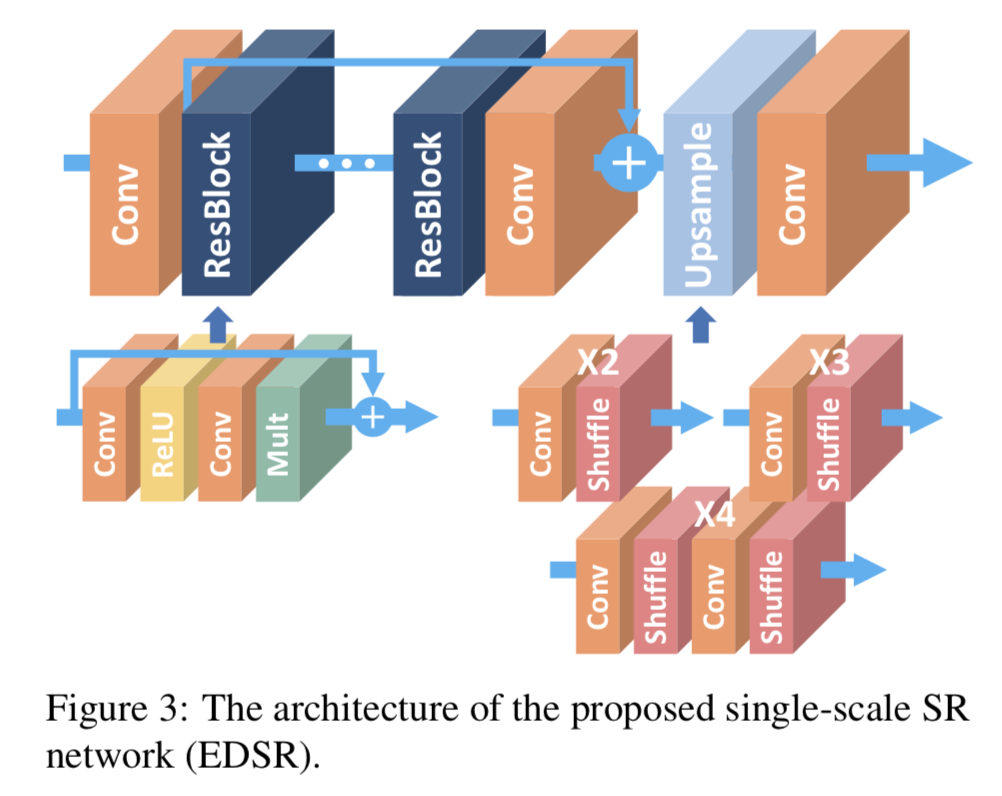
原文中提到,原始的ResNet最一开始是被提出来解决高层的计算机视觉问题,比如分类和检测,直接把ResNet的结构应用到像超分辨率这样的低层计算机视觉问题,显然不是最优的。由于批规范化层消耗了与它前面的卷积层相同大小的内存,在去掉这一步操作后,相同的计算资源下,EDSR就可以堆叠更多的网络层或者使每层提取更多的特征,从而得到更好的性能表现。EDSR用L1范数样式的损失函数来优化网络模型。在训练时先训练低倍数的上采样模型,接着用训练低倍数上采样模型得到的参数来初始化高倍数的上采样模型,这样能减少高倍数上采样模型的训练时间,同时训练结果也更好。
训练结果给的是2、3、4倍,效果依次递减。也就是2倍的PSNR和SSIM效果是最好的。
文中同时还给出了一个能同时进行不同上采样倍数的网络结构MDSR:
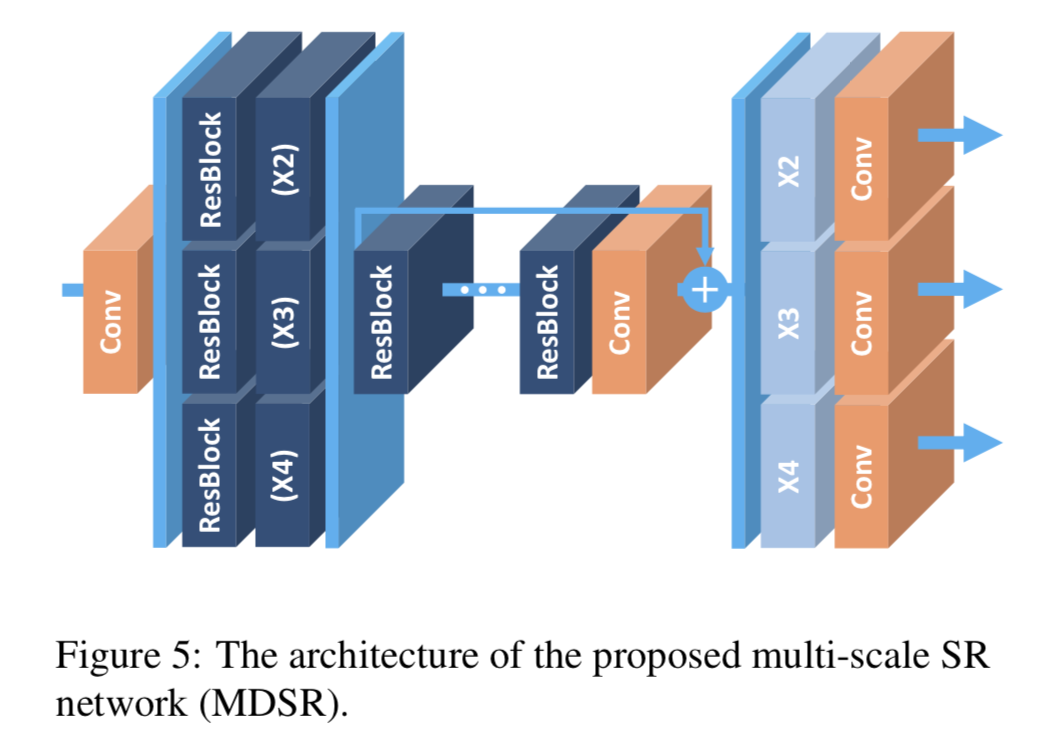
链接:见4.2.2节。
code:https://github.com/jmiller656/EDSR-Tensorflow 、https://github.com/thstkdgus35/EDSR-PyTorch 、https://github.com/LimBee/NTIRE2017
PULSE
PULSE: Self-Supervised Photo Upsampling via Latent Space Exploration of Generative Models
来自2020年CVPR,一篇非常amazing的文章:PULSE最多能将16*16放大至1024*1024,即64倍放大。
Starting with a pre-trained GAN, our method operates only at test time, generating each image in about 5 seconds on a single GPU.
传统方法处理此类问题时,一般拿到LR图像后,会“猜测”需要多少额外的像素,然后试着将此前处理过的HR图像中相应的像素,匹配给LR图像。而这种单纯匹配像素的结果是,像头发和皮肤的纹理这种区域,会出现像素匹配错位的现象。而且该方法还会忽略了HR图像中,感光性等感知细节。所以最终在平滑度、感光度上出现问题,结果依然会显得模糊或者不真实。
PULSE则给出了一个新的思路:在拿到一张LR图像后,PULSE系统不会慢慢添加新的细节,而是遍历GAN生成的HR图像,将这些HR图像对应的LR图像与原图对比,找到最接近的那张。实际上就是用LR图片做反推导:找到最相似的LR版本,那么再反推回去,这张LR图像所对应的HR图像,就是最终要输出的结果。

使用的基本模型是GAN。在复原的过程中,该网络会“想象”出一些原本不存在的特征,即使是原本LR照片中无法看到的细节,比如毛孔、细纹、睫毛、头发和胡茬等,经过其算法处理后,都能看得一清二楚。
实验结果:在著名的高分辨率人脸数据集CelebA HQ用64×,32×和8×的比例因子进行了这些实验。并要求40个人对通过PULSE和其他五种缩放方法生成的1440张图像进行MOS评分,PULSE的效果最佳,得分几乎与真实的高质量照片一样高。
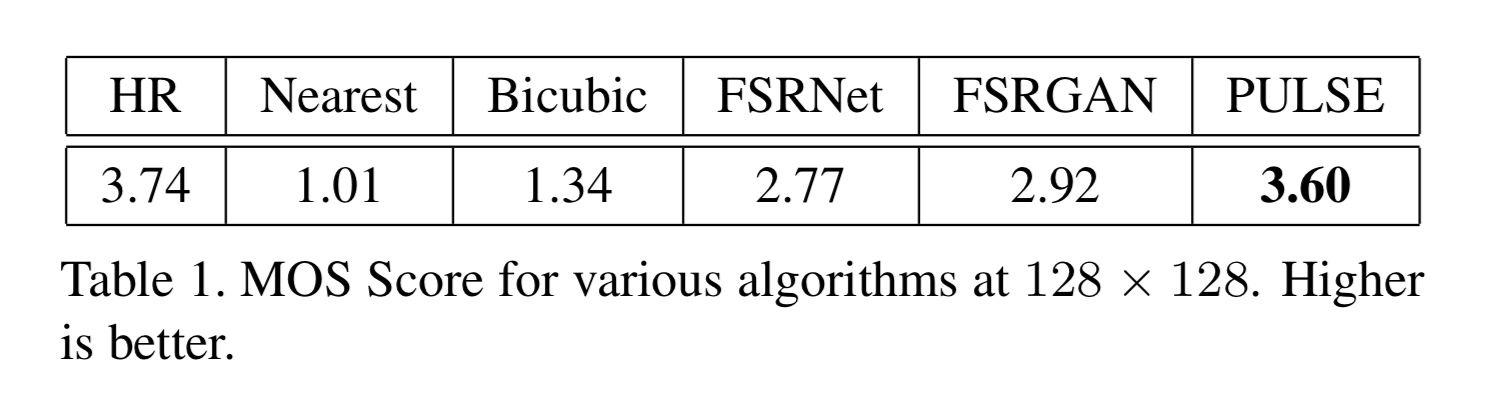
对不同类型的人脸的复原Success rates也做了统计:

比较在意的人像位置:头发、眼睛、嘴唇:

该模型有如下局限性:
- 只针对人脸(虚幻脸);
We show extensive experimental results demonstrating the efficacy of our approach in the domain of face super-resolution (also known as face hallucination).
However, we also note significant limitations when evaluated on natural images past the standard benchmark.
- 不能用于识别身份:无法将安全摄像头拍摄的失焦、不能识别的照片,变成真人的清晰图像。
意思就是说仅会生成不存在但看上去很真实的新面孔。
链接:https://arxiv.org/pdf/2003.03808.pdf
code:https://github.com/adamian98/pulse
其他
常用的Image SR评价指标
PSNR
峰值信噪比(Peak Signal to Noise Ratio,PSNR)是一种极其普遍且在各个领域进行图像处理工作时都广泛使用的评估图像质量的客观量测法。评价的指向为经过压缩、降噪等操作后的图像,相对于原图像的噪声强度。失真程度越大,该指标给出的值就越小。
给定不含噪声的图像I(大小为M*N)和带有噪声的图像K,将均方误差MSE定为:
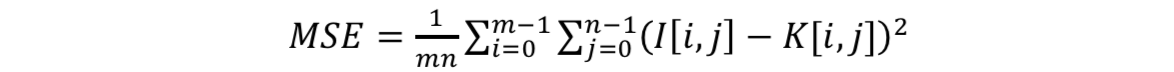
PSNR则定义为:
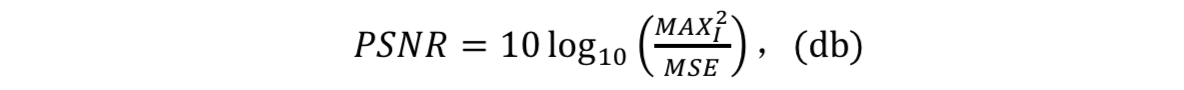
作为一种客观的评价指标,众多的实验都指出,PSNR同人的眼睛所看到的图像的视觉品质的主观评价是由很大出入的,也就是说,PSNR评分高的图像,在人眼的主观评价中,反而可能不如PSNR低分图像。实际上该指标并未考虑视觉评价的感知特性。
SSIM
结构相似性(Structural Similarity index,SSIM)是对比两图相似程度的指标。SSIM分别使用协方差、均值和标准差作为图片的结构相似程度、亮度和对比度的评价指标,这三个因素共同组合成图片失真程度的评价。三个评价的范围都是从0到1,无单位。若进行评价的两张图像完全相同,SSIM就会等于1。
给定进行对比的两张图像x和y,SSIM定义为:
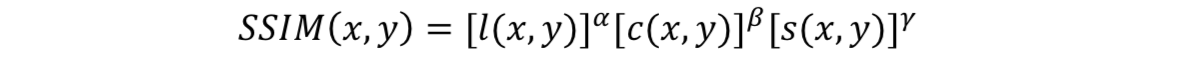
其中,α,β,γ>0,l(x,y)是亮度的评价,c(x,y)是对比度的评价,s(x,y)是结构的评价。
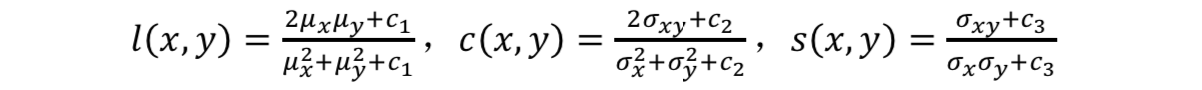
c1,c2,c3均为非零常数,μ为均值,σ为方差和协方差。在实际工程计算中,一般设定α,β,γ=1,c3=c2/2。
SSIM具有对称性,即SSIM(x,y)=SSIM(y,x)。
SSIM是视频及图像质量评估的一种常见且效果良好的算法,不过它依久具有同PSNR相似的缺陷。
NTIRE
NTIRE英文全称是New Trends in Image Restoration and Enhancement,也就是“图像恢复与增强的新趋势”,是近年来计算机图像修复领域最具影响力的一场赛事,每年都会吸引大量的关注者和参赛者。
该比赛自2017年开始第一届,到今年已经举办了四届。2017年该比赛共拥有三个赛道,而今年的比赛增加到了5个赛道(2020.6比赛结果已出),分别是:
2020年赛道
Real-World Image Super-Resolution
经典赛道,自2017年开始就有的图像超分辨率。
Image Dehazing
经典赛道,自2017年开始就有的图像去雾。
Image Demoireing
图像去摩尔纹,是今年的新赛道。
摩尔纹是一种在数码照相机或者扫描仪等设备上,感光元件出现的高频干扰的条纹,是一种会使图片出现彩色的高频率不规则的条纹。
Spectral Reconstruction from an RGB Image
该任务的目的是从RGB图像中重建全场景高光谱(HS)信息。
Video Quality Mapping
该挑战拟解决从源视频域到目标视频域的质量映射问题。挑战包括两个子任务:监督轨道和弱监督轨道。 其中,轨道1提供了一个新的Internet视频基准数据集,要求算法以监督训练的方式学习从压缩程度更高的视频到压缩程度更低的视频间的映射关系。 在轨道2中,需要算法来学习从一个设备到另一个设备的质量映射关系。
Image SR赛道冠军论文
2017
EDSR
Enhanced Deep Residual Networks for Single Image Super-Resolution
2018
WDSR
Wide Activation for Efficient and Accurate Image Super-Resolution
2019
UDSR
2020
Real-World Super-Resolution via Kernel Estimation and Noise Injection
NTIRE中Image SR赛道结果综述
Single Image SR -> Real Image SR -> Real-World Image SR
从最开始的模拟下采样(Bicubic)图像到现在的Real-World Image,可见现在的挑战任务越来越走向通用化和实用化,当然这也意味着难度的升级。
NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results
NTIRE 2018 Challenge on Single Image Super-Resolution: Methods and Results
NTIRE 2019 Challenge on Real Image Super-Resolution: Methods and Results
NTIRE 2020 Challenge on Real-World Image Super-Resolution: Methods and Results
Image SR相关资源(持续更新)
2000-2020的Image SR文献总结:https://github.com/YapengTian/Single-Image-Super-Resolution
CVPR2020|图像重建(超分辨率,图像恢复,去雨,去雾,去模糊,去噪等)相关论文汇总:https://blog.csdn.net/Kobaayyy/article/details/106815083
