原创文章,转载、引用请注明出处!
Learning a Deep Convolutional Network for Image Super-Resolution
SRCNN是深度学习用在超分辨率重建上的开山之作。
网络结构
SRCNN的网络结构非常简单,仅仅用了三个卷积层,网络结构如下所示:
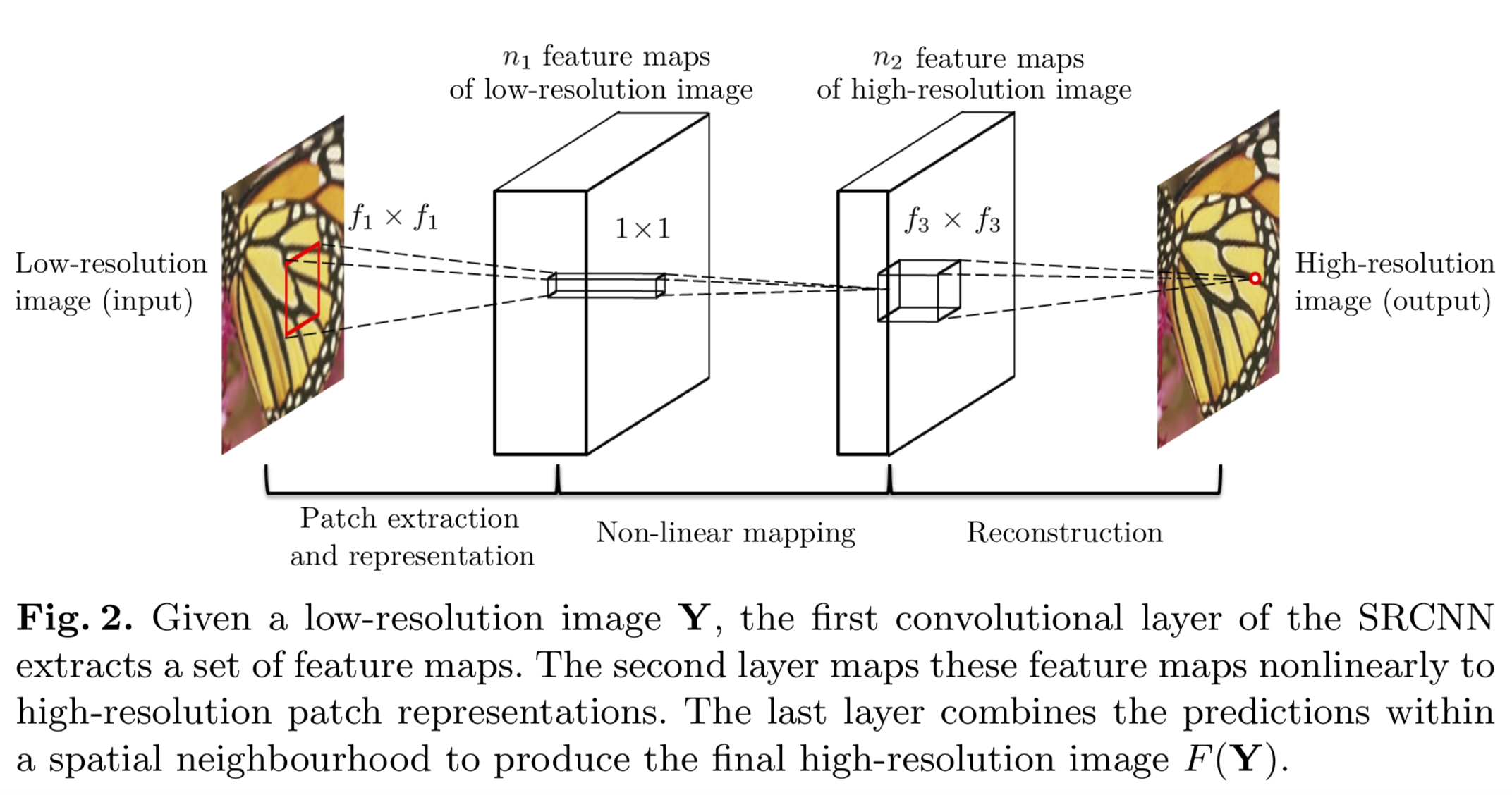
SRCNN网络包含三个模块:Patch extraction and representation(块析出与表示)、Non-linear mapping(非线性映射)、Reconstruction(重构)。这三个模块对应三个卷积操作。
第一层CNN:对输入图片的特征提取。(9x9x64卷积核);
第二层CNN:对第一层提取的特征的非线性映射(1x1x32卷积核);
第三层CNN:对映射后的特征进行重建,生成高分辨率图像(5x5x1卷积核)。
在进行卷积操作之前,SRCNN对图像进行了一个预处理:将输入的低分辨率图像进行bicubic插值,将低分辨率图像放大成目标尺寸。接下来才是上面提到的三层卷积网络拟合非线性映射,最后输出高分辨率图像结果。
插值后的图像依旧称为“低分辨率图像”,并用Y表示;将ground-truth(真实的高分辨率图像)用X表示;将网络记为映射函数F(·);
网络的总思路来源于稀疏编码,作者将上述三个过程表述为:
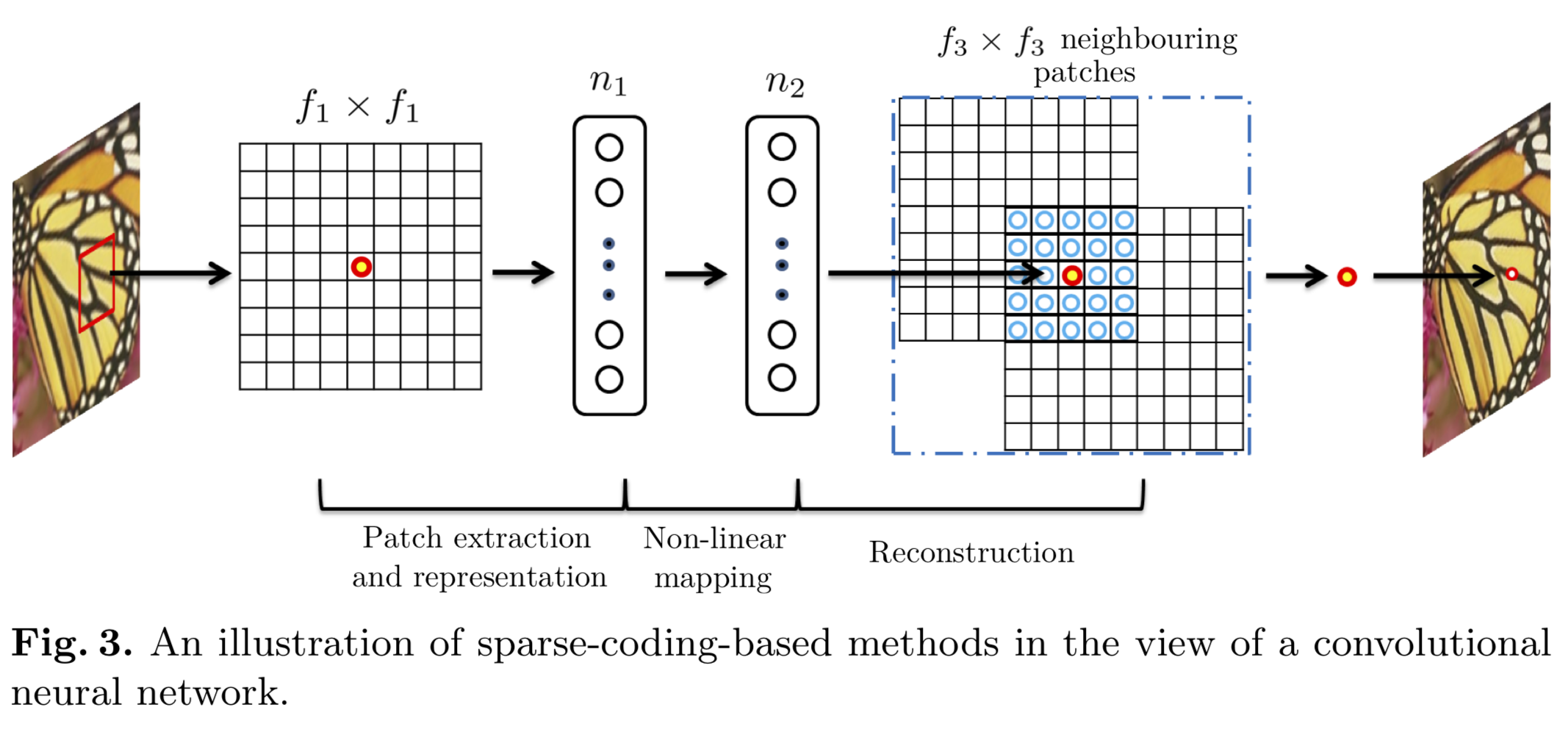
Patch extraction and representation
块析出和表示的目的是通过输入图像Y获得一系列特征图:
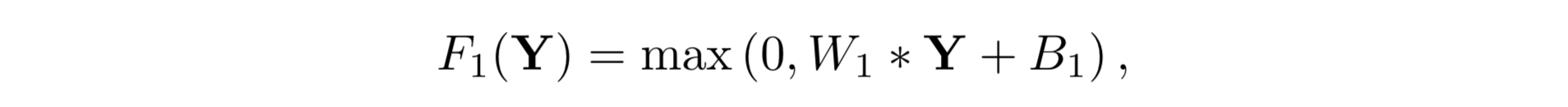
其中W1和B1表示滤波器(卷积核)的权重和偏置,max操作对应ReLU激活函数。
Here W1 is of a size c × f1 × f1 × n1, where c is the number of channels in the input image, f1 is the spatial size of a filter, and n1 is the number of filters.
B1 is an n1-dimensional vector, whose each element is associated with a filter.
卷积+激活操作。
Non-linear mapping
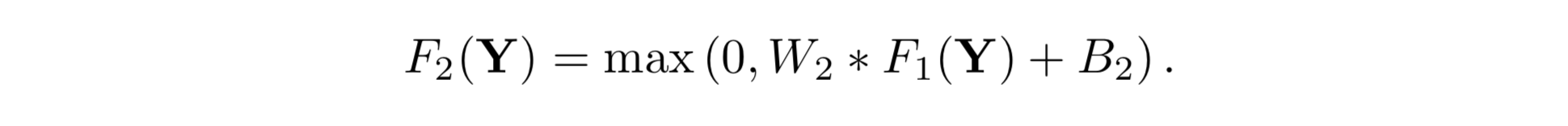
其中W2和B2表示滤波器的权重和偏置,max操作依旧对应ReLU激活函数。
第二层和第一层的思路完全一致,实际上这里想表述的是可以添加更多的层,但是这样的操作会显著增加网络的计算开销。
It is possible to add more convolutional layers (whose spatial supports are 1× 1) to increase the non-linearity. But this can significantly increase the complexity of the model, and thus demands more training data and time. In this paper, we choose to use a single convolutional layer in this operation, because it has already provided compelling quality.
Reconstruction
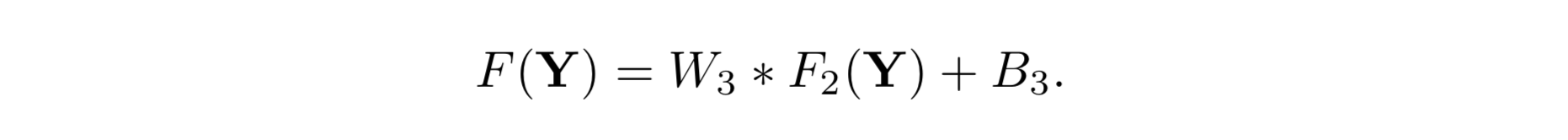
Here W3 is of a size n2 ×f3 ×f3 ×c, and B3 is a c-dimensional vector.
W3:线型滤波器we expect that W3 behaves like first projecting the coefficients onto the
image domain and then averaging. In either way, W3 is a set of linear filters.
重构依旧是卷积操作,但是这里没有激活函数了。
根据上面的三个公式,SRCNN仅有6个需要学习的参数:W1、B1、W2、B2、W3、B3。
损失函数
损失的计算也仅仅需要网络的输出F(Y)与真实高分图像X,损失函数选择MSE损失:
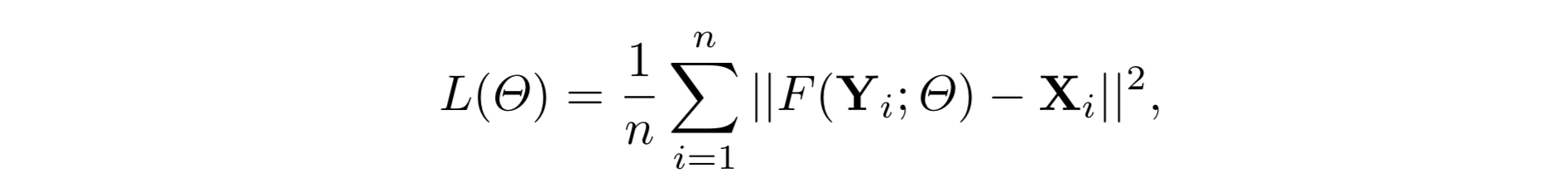
选择MSE作为Loss的原因:有利于提高PSNR。
Using MSE as the loss function favors a high PSNR.
实际上,卷积神经网络对损失函数的限制只有一个,即损失函数为可导函数。如果在训练过程中给出一个更好的感知激励指标,则网络可以灵活地适应该指标。但原文提到“会做研究但很难实现”。
The PSNR is a widely-used metric for quantitatively evaluating image restoration quality, and is at least partially related to the perceptual quality. It is worth noticing that the convolu- tional neural networks do not preclude the usage of other kinds of loss functions, if only the loss functions are derivable. If a better perceptually motivated metric is given during training, it is flexible for the network to adapt to that metric. We will study this issue in the future. On the contrary, such a flexibility is in general difficult to achieve for traditional “hand-crafted” methods.
结论
实验结论
分别以Running Time和PSNR为指标并与多种方法进行了对比实验。
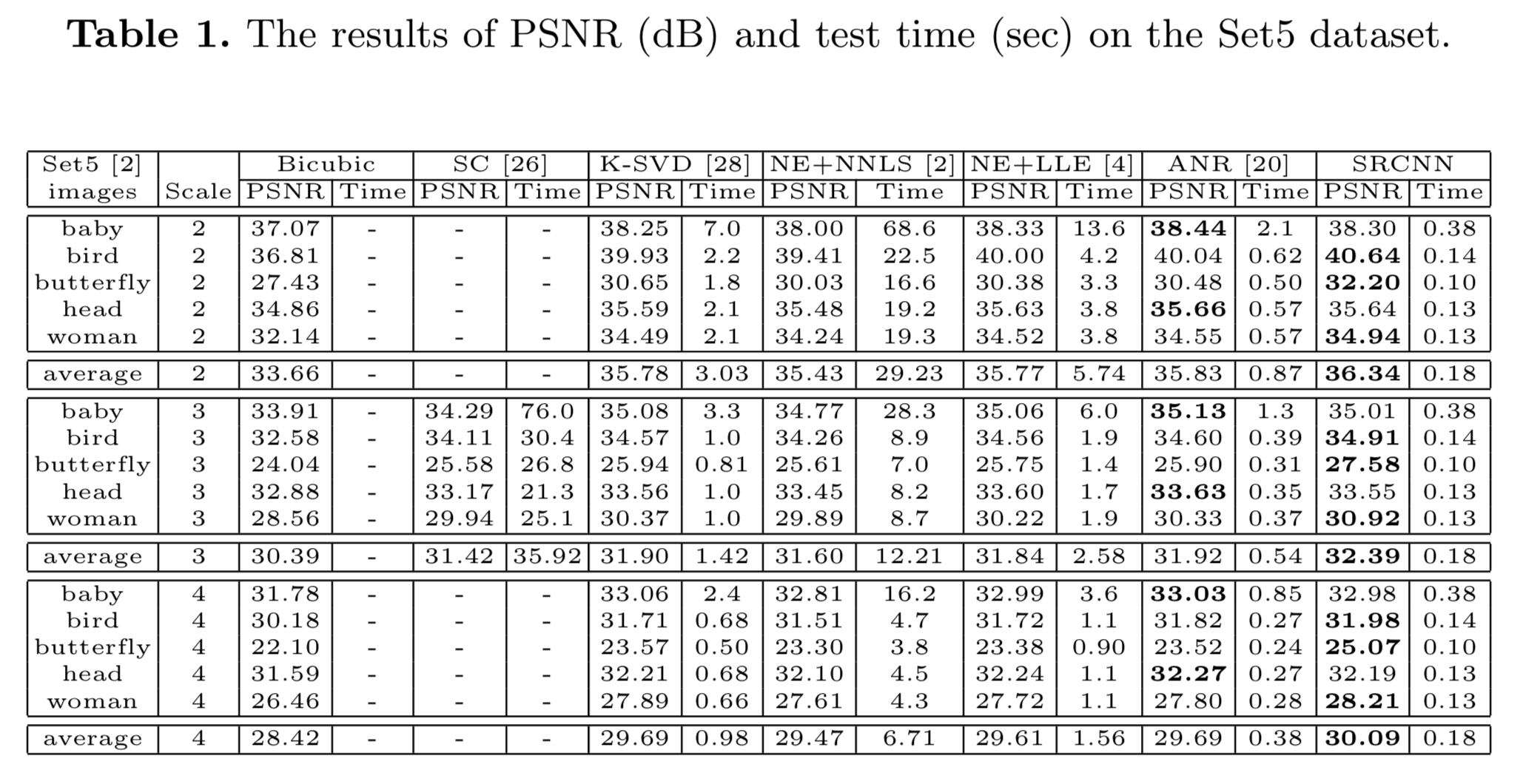
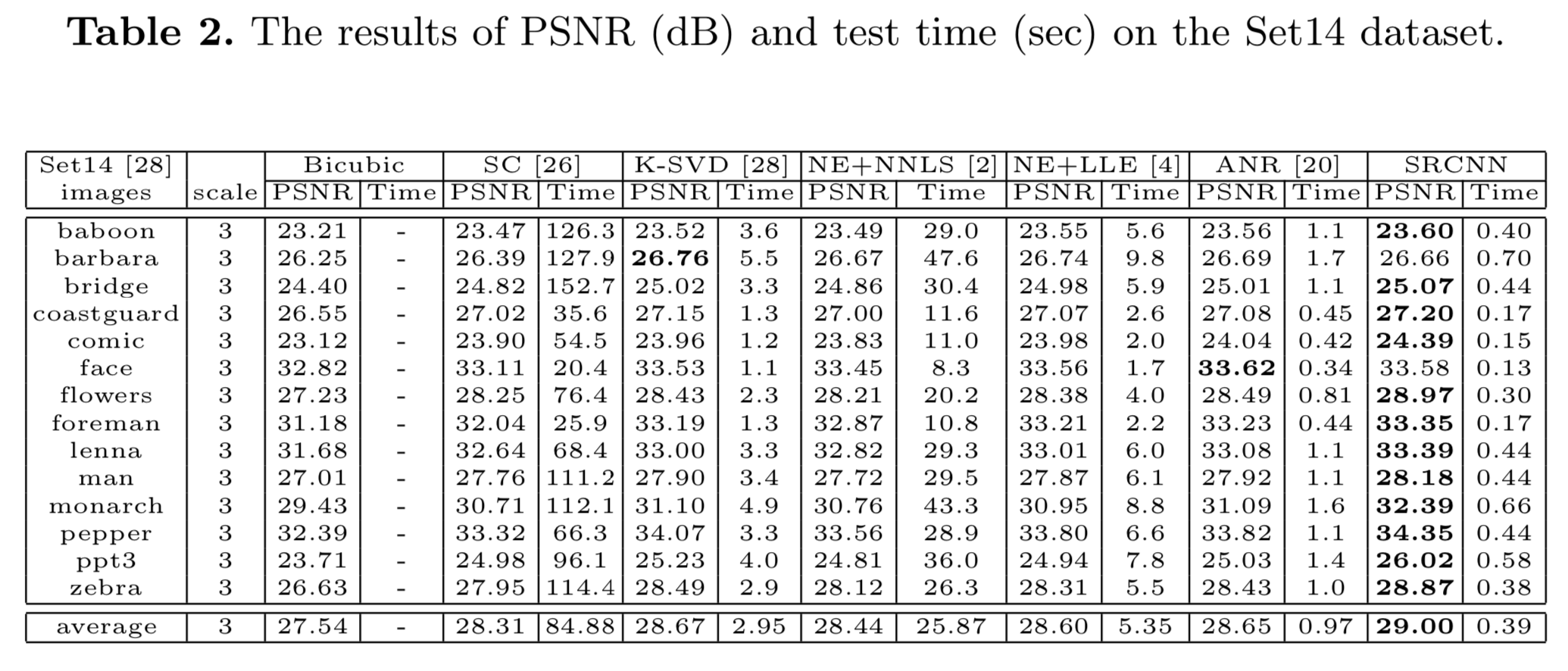
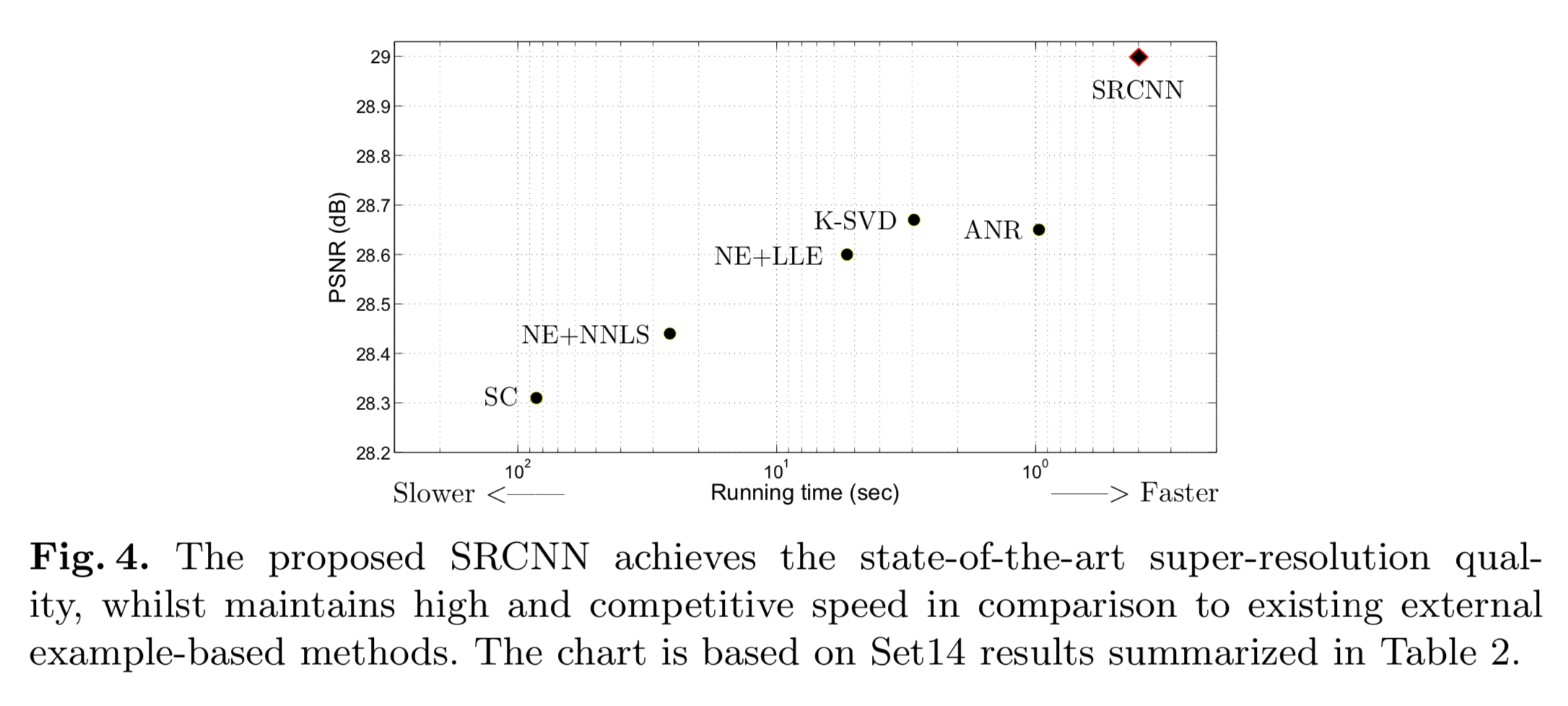
SC:sparse coding,稀疏编码
Image super-resolution via sparse representation, 2010
K-SVD
On single image scale-up using sparse representations, 2012
NE+LLE:neighbour embedding + locally linear embedding,邻域嵌入+局部线性嵌入
Super-resolution through neighbor embedding, 2004
NE+NNLS:neighbour embedding + non-negative least squares,邻域嵌入+非负最小二乘法
Low-complexity single image super-resolution based on nonnegative neighbor embedding, 2012
ANR:Anchored Neighbourhood Regression,锚定邻域回归
Anchored neighborhood regression for fast example-based super-resolution, 2013


给出了4个种类的图片的SR结果及对比。原文中提到,在“baby”的类别上PSNR并未达到最好的效果。以下给出两组。
经典的“Butterfly”和原文中提到的PSNR不达标的“Baby”。
In spite of the best average PSNR values, the proposed SRCNN does not achieve the highest PSNR on images “baby” and “head” from Set5. Nevertheless, our results are still visually appealing (see Figure 10).
模型对数据量的敏感性
文章使用SRCNN分别在ImageNet和Timofte数据集这两个数据集上分别进行了实验。在ImageNet上获得的PSNR值明显高于在Timofte数据集上的结果。这里的结论是:在迭代次数相同的情况下,数据量的增加可能会提高网络的性能。
模型对卷积核数量的敏感性
SRCNN中第一层包含n1=64个卷积核,第二层包含n2=32个卷积核。根据理论,增加网络的卷积核数量必然会提升模型的性能。
作者尝试做了额外的增加以及减少卷积核数量两种情况:

从上表可以看出,增加卷积核数量确实会获得更高的PSNR值,但是同时会增加计算时间。所以需要在时间和质量之间做一个权衡。
其他
训练数据集:Timofte数据集(包含91幅图像)和ImageNet数据集(数据量超大);
文章:http://personal.ie.cuhk.edu.hk/~ccloy/files/eccv_2014_deepresolution.pdf ;
code:http://mmlab.ie.cuhk.edu.hk/projects/SRCNN.html ,有matlab版本和Caffe版本;
文章比较简单,内容都在字面上,比较好理解。方法超前但是借鉴的痕迹很重,因此没有那种“专事专办”的味道。
