原创文章,转载、引用请注明出处!
Wavelet-SRNet: A Wavelet-based CNN for Multi-scale Face Super Resolution
2017年的一篇文章,核心论点是小波变换+CNN,针对的问题是人脸的SR。
立意
文章提出,在对低分辨率图像做上采样的时候,传统CNN方法的问题:
性能的降低;
输出过于平滑,导致了细节遗失(翻译成白话就是上采样的主观效果差);
When dealing with very low resolution (LR) images, the performance of these CNN based methods greatly degrades. Meanwhile, these methods tend to produce over-smoothed outputs and miss some textural details.
深度学习类的方法,导致过度平滑的原因:使用MSE作为loss。
Most of these convolutional methods use MSE loss to learn the map function of LR/HR image pairs, which leads to over-smooth outputs when the input resolution is very low and the magnification is large.
- 低倍数下才有良好的效果。
Besides, they seem to only work well on limited up-scaling factors (2× or 4×) and degrades greatly when ultra-resolving a very small input (like 16 × 16 or smaller).
网络结构
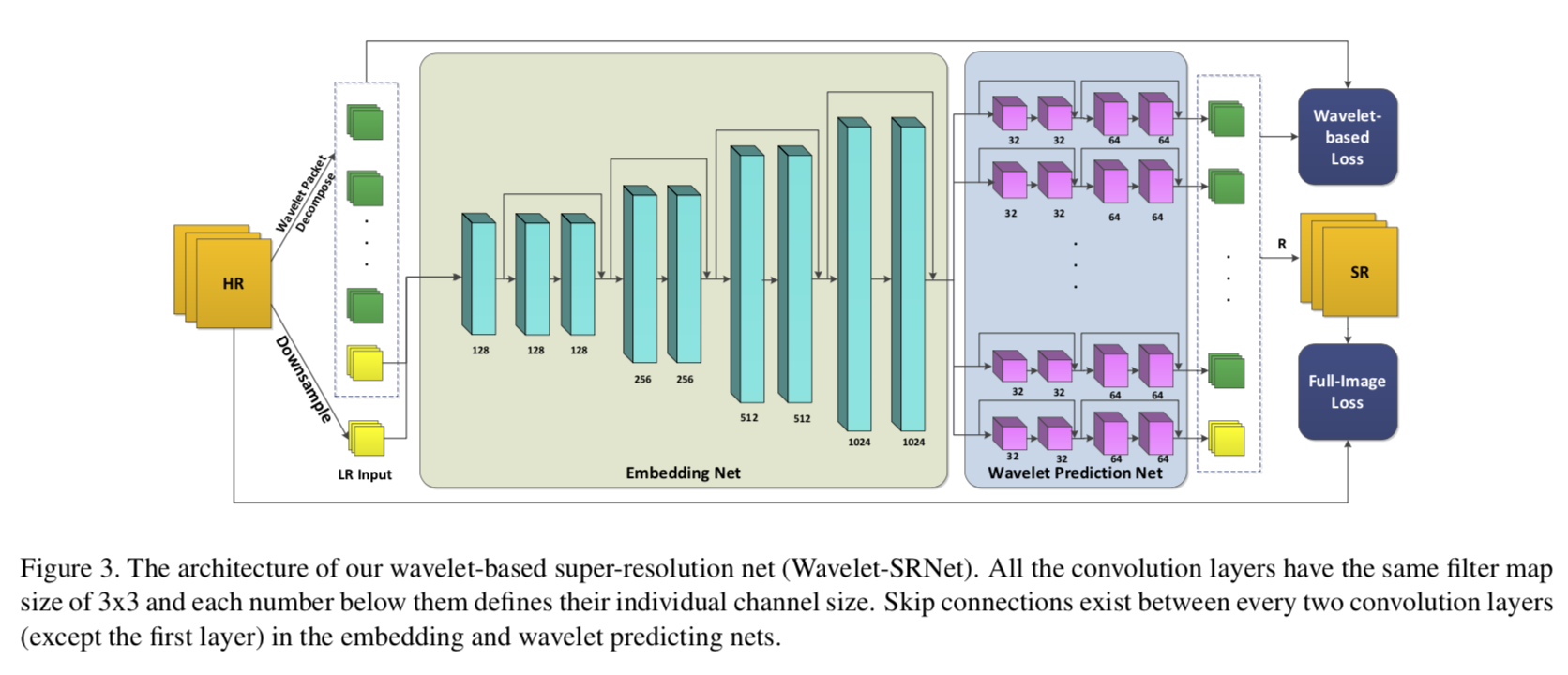
HR图像在输入Wavelet-SRNet之前首先会做小波包分解:通过小波包分解将图像解析为一组具有相同大小的小波系数:

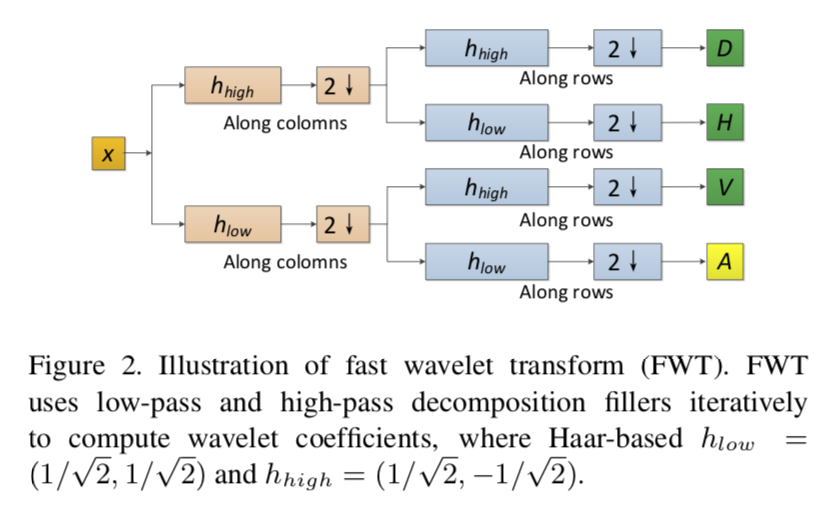
Wavelet-SRNet选用最简单的小波:haar小波,此小波足以描述不同频率的人脸信息。另外,使用快速小波变换(2-D fast wavelet transform ,FWT)来计算haar小波:
Wavelet-SRNet分为三个子网:
embedding
embedding网络的作用是将低分辨率输入表示为一组特征地图。
嵌入网络以3×h×w的低分辨率图像为输入,将其表示为一组特征映射。所有卷积的大小都是相同的3×3,步长为1,pad为1,使得嵌入网络中的每个特征图与输入图像的大小相同。
通过embedding网络,将输入的LR图像映射成Ne×h×w的特征映射,不需要上采样或下采样,其中Ne是最后一层的信道尺寸。
wavelet prediction
经过embedding网络之后,利用小波预测网对相应的小波系数图像进行估计。
将小波包分解到小波网络的每一个子网中,并将小波包分解成相应的小波网络。这里将所有3×3的卷积填充物设置为步长为1、pad为1的卷积(与embedding网络相似),使得每个推导出的小波系数与LR输入的大小相同,即3×h×w。
此外,由于Haar小波变换系数之间的高度独立性,每两个子网之间不允许任何信息交互,这使得我们的网络具有可扩展性。
可扩展性:wavelet prediction net中的子网数量Nw可根据需求进行调整。
在预测网中,用不同的子网数目很容易实现不同的放大倍数。例如,Nw=16和Nw=64分别代表4倍和8倍的放大倍数。
reconstruction networks。
最后,重建网络从这些系数图像重建出高分辨率图像。
利用重构网络将总尺寸为Nw×3×h×w的小波图像变换成3×(r×h)×(r×w)的原始图像空间。由一个填充尺寸为r×r,步长为r的解卷积层(deconvolution)组成。
虽然解卷积层的大小取决于放大倍数r,但它可以由一个常数小波重构矩阵初始化并在训练中固定。因此,它对整个网络的可扩展性没有影响。
最后,三个子网络之间的输入输出映射关系:
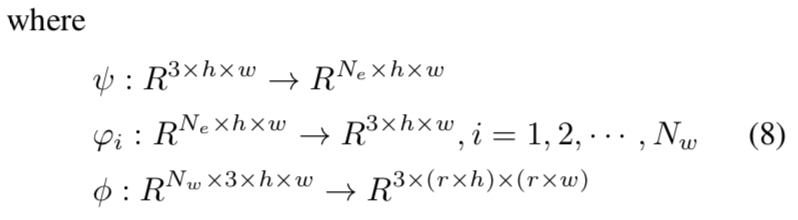
损失函数
整个loss函数分为三部分:
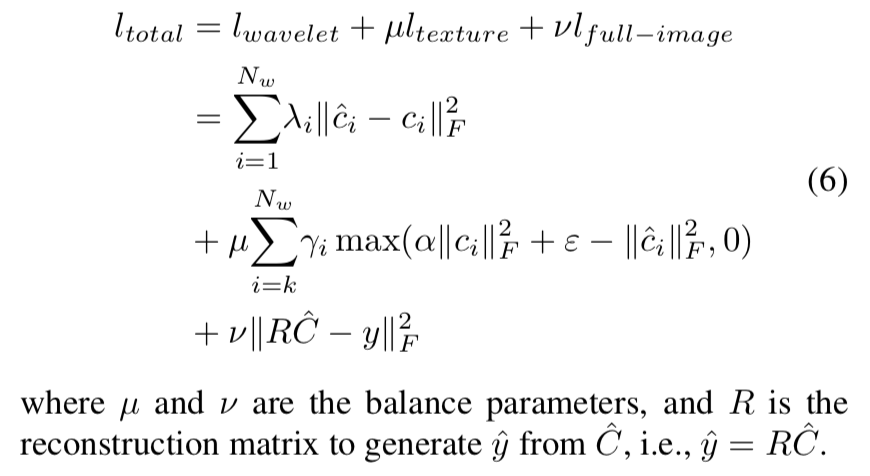
full-image loss(MSE)
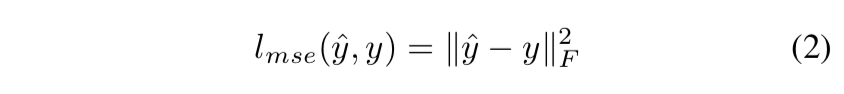
MSE是超分辨率方法中最常使用MSE损失函数。
MSE是在图像空间上的一个限制,因为MSE几乎不能获取到高频纹理细节信息。Wavelet-SRNet的full-image loss一方面是在图像空间上的限制,另一方面也能在平滑度和纹理细节上达到一个平衡。
A traditional MSE loss in image space, which is called full-image loss, is also used to get a balance between s- moothness and textures.
wavelet-based loss
这里同样分为两部分:
wavelet prediction loss
wavelet prediction loss相当于在小波域上的加权MSE,定义如下:
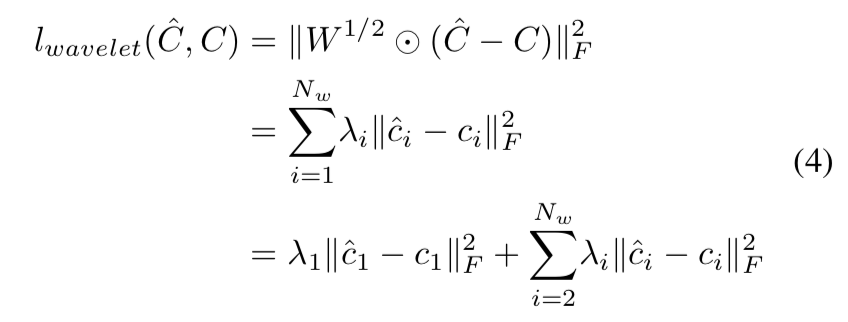
W=(λ1,λ2,⋅⋅⋅,λNw),一个平衡不同组小波系数重要性的权重矩阵;C是真实值,C尖是小波系数;绝对值的项用来提取全局拓扑信息
这个loss函数应该更关注局部纹理信息,故高频系数的权重应该更大一点。
The former one is a weight- ed version of MSE in wavelet domain…… More attention can be paid on local textures with bigger weights appointed to high-frequency coefficients.
texture loss
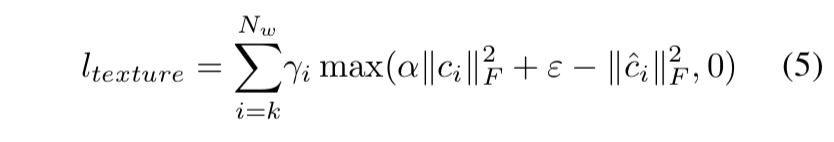
texture loss是为了避免高频小波系数收敛为0。α和ϵ是slack values,可以使高频小波系数不为0,因此避免了纹理细节的下降。
The texture loss is designed to prevent high-frequency wavelet coefficients from converging to zero….. It keeps high-frequency wavelet coefficients non-zero and hence prevents the degradation of texture details.
实验
实验细节
输入的LR图片做了一组对比:一组是双三次插值,一组是小波包变换的近似系数。
Two types of low-resolution images are taken as input, one of which is down-sampled by bicubic interpolation and the other is the approximation coefficient of wavelet packet decomposition.
模型可适应任意大小的输入,因为没有全连接层。
Since our network is a fully convolutional architecture without fully-connected layers, it can be applied to the input of arbitrary size.
给出了网络的设置。
Our model is implemented with the Caffe frame- work [11]. The loss in (6) is minimized using SGD with a batch size of 256. For the hyper-parameters, we set em- piricallyλ1 = 0.01,λ2 = λ3 = ··· = λNw = 1,μ = 1,k=2,γk =γk+1 =···=γNw =1,ν=0.1. The learning rate is set to 0.01 initially and reduced by a factor of 10 each 3000 iterations. It takes about 14, 000 ∼ 16, 000 iterations for our network to converge.
两个数据集做训练。
Our experiments are implemented on two datasets: CelebA and Helen. There are 202,599 faces in CelebA and 2,230 faces in Helen. In the training phase, we use the large train set of CelebA(162,700 images) for training and the validation set(19,867 images) of CelebA for validation. In the testing phase, we evaluate with the 19,962-image test set of CelebA and the 330-image test set of Helen, assuring no over-lapped images appearing in both the training and testing phase. The images are cropped around the face with eyes aligned horizontally.
为了保证对照训练的公平,所有的数据集都使用了眼睛对齐的人脸照片,且在下采样之前没有做其他额外的处理。
For a fair comparison, we use the same set of eyes-aligned faces for all the methods with no extra preprocessing before down-sampling.
使用的评价指标:SSIM和PSNR。
We adopt PSNR(dB) and SSIM for quantitative metric, and calculate PSNR on the luminance channel, following by [35], and SSIM on the three channels of RGB.
实验结果
不同放大倍数的定性比较
与双三次插值对比了不同放大倍数下的效果。

不同方法的定性比较
8倍放大下不同方法的对比。

鲁棒性讨论
讨论了模型在面对未知高斯模糊,姿态和遮挡的鲁棒性。
在图6中,低分辨率人脸由高斯模糊核生成,其步长为8,对应于8×下采样。高斯模糊核的σ从0增加到6,其中σ=0表示最近邻插值下采样。如图6所示,当σ<4时,模型方法显示出一定的鲁棒性,当σ>=4时生成更平滑的面。

作为比较,CBN的结果与平均面更接近。对于姿态变化,如图7所示,CBN无法重建大姿态的可信人脸,可能是由于空间预测不准确。

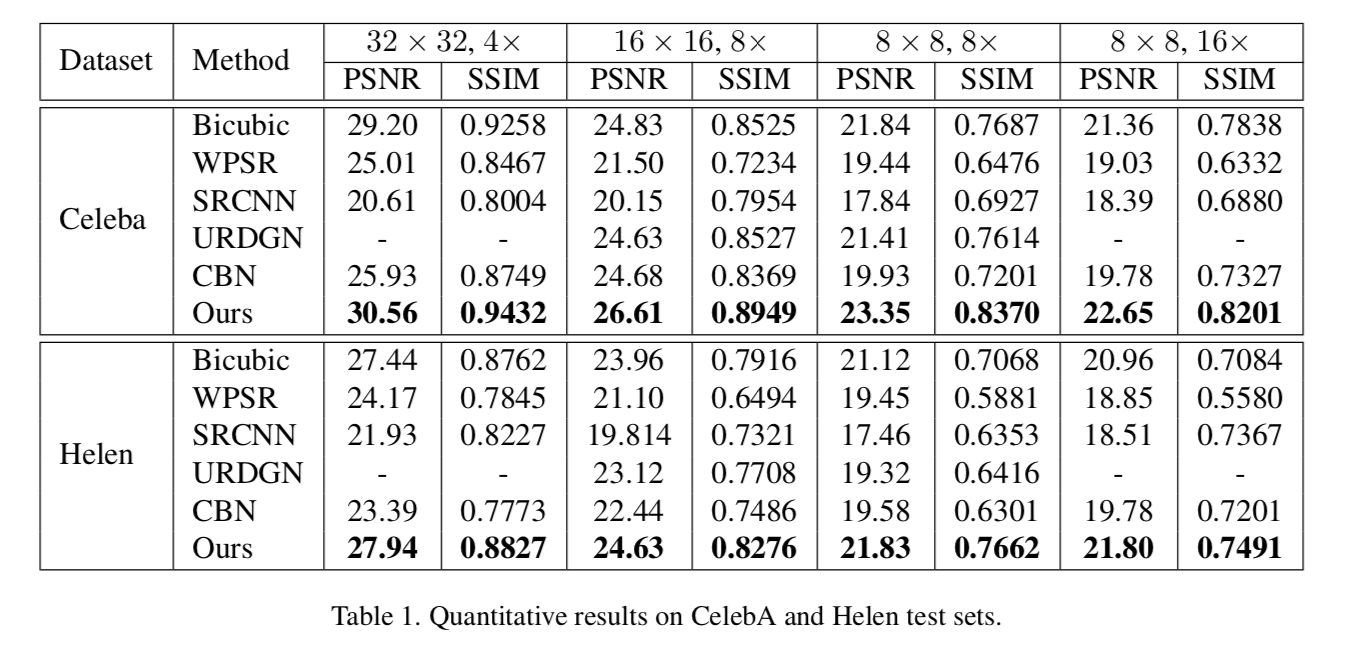
不同放大倍数的定量比较
四个放大倍数:(32×32,4×),(16×16,8×),(8×8,8×)以及(8×8,16×),其中(m×m,n×)为m×m输入分辨率,放大倍数为n。
贡献
来自原文的叙述:
- A novel wavelet-based approach is proposed for
CNN-based face SR problem. To the best of our knowledge, this isthe firstattempt to transform single image SR to wavelet coefficients prediction task in deep learning framework - albeit many wavelet-based researches exist for SR.
- A novel wavelet-based approach is proposed for
- A flexible and extensible fully convolutional neural network is presented to make the best use of wavelet transform. It can apply to different input-resolution faces with multiple upscaling factors.
- We qualitatively and quantitatively explore multiscale face super-resolution, especially on
very low input resolutions. Experimental results show that our proposed approach outperforms state-of-the-art face SR methods.
- We qualitatively and quantitatively explore multiscale face super-resolution, especially on
其他
感想
第一次用了小波包变换和深度的结合在这个问题上,有开创意义。
放大倍数方面,文章给出了32,对模型的描述是:可以接受任何大小的数据以及可拓展性。意思就是说放大的倍数也是比较有前景的(如果效果真的像叙述的一样有力的话)。
做的问题是有针对性的,就是正面、无任何遮挡或者偏移的人脸。
后面在做鲁棒性的讨论时,也凸显出了模型的局限性(实际上就是给出了大家都无法解决的问题)。
小波变换
一种进行信号时频分析和处理的方法。
理论依据:傅里叶变换 -> 短时傅里叶变换 -> 小波变换
这三种变换的本质是将信号从时域转换为频域。上面的论文里用到的:小波包变换,由小波变换而来
傅立叶变换(FT)
傅里叶变换的核心是从时域到频域的变换,而这种变换是通过一组特殊的正交基来实现的。
如何理解傅里叶变换公式? - 苗华栋的回答 - 知乎
https://www.zhihu.com/question/19714540/answer/1119070975
傅立叶变换的三个核心:
傅立叶的重要论断:任何连续周期信号都可以由一组适当的正弦曲线组合而成。
为什么要变换?因为最容易理解的表现形式不一定是最方便做计算的。变换(计算空间)的意义是将原来空间中难以处理的问题变换到方便计算的空间去。
变换的空间是什么?时域和频域。
短时傅立叶变换(STFT)
傅立叶变换的缺陷
在傅立叶变换的基础上提出新的讨论,是因为傅立叶变换是有缺陷的:对非平稳过程,傅里叶变换有局限性。
再进一步的说明是,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
然而平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的。对于这样的非平稳信号,只知道包含哪些频率成分是不够的,我们还想知道各个成分出现的时间。理解信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值,也就是时频分析。
加窗
想到知道频率随时间变化的情况,一个简单的思想就是“加窗”:把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。
短时傅立叶变换的基本思想由此而来:将信号加滑动时间窗,并对窗内信号做傅立叶变换,得到信号的时变频谱。
小波变换(WT)
短时傅立叶变换的缺陷
同上,新的讨论一定是因为前者有缺陷:提到了加窗,那么问题就是,这个“窗函数”如何定义?窗太宽太窄都会出现问题:窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差。窗太宽,时域上又不够精细,时间分辨率低。
所以窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。
可变窗的STFT
一种解决上述问题的方法是:让窗口大小变起来,多做几次STFT不就可以了吗?
小波变换就有着这样的思路,但事实上小波并不是这么做的。至于为什么不采用可变窗的STFT呢,有很多解释,公认的缺陷是这样做的话STFT做不到正交化。
大部分的解释里有这样的说法:小波变换能够提供一个随频率改变的“时间-频率”窗口。这也是一种理解性的说法,通过改变基底做到了可变窗,重点应该是基底的改变。
改变基底
小波变换的出发点和STFT还是不同的:直接把傅里叶变换的基底做了改变,将无限长的三角函数基换成了有限长的会衰减的小波基。
小波变换就是为了解决对非平稳信号的分解问题而产生的数学方法。相比于傅里叶变换使用一组无限长的三角函数基进行信号拟合,小波变换使用的是一组正交的、迅速衰减的小波函数基进行信号拟合。这种小波函数基可通过其尺度变量和平移变量,获得不同的频率和时间位置。因此在利用这种小波函数基对信号进行分解时,可以用较少的小波函数基就拟合出突变信号(稀疏编码特性),同时也能获得不同频率的信号分量在时域上的出现位置。
WT的总体理解
小波变换是这样一个过程:首先将原始信号作为输入信号,通过一组正交的小波基分解成高频部分和低频部分,然后将得到的低频部分作为输入信号,又进行小波分解,得到下一级的高频部分和低频部分,以此类推。随着小波分解的级数增加,其在频域上的分辨率就越高。这就是多分辨率分析(MRA,MultiResolution Analysis)。
从数学的角度理解,在小波变换中,一个位于希尔伯特空间中的函数,可以分解成一个尺度函数和一个小波函数,其中尺度函数对应原始函数中的低频部分,小波函数对应原始函数中的高频部分。通过尺度函数可以构建对原始信号的低通滤波器,通过小波函数可以构建对原始信号的高通滤波器。
希尔伯特空间:完备的内积空间。
Linear Space → Normal Linear Space → Banach Space
Normal Linear Space → Inner Product Space
→ Banach SpaceInner Product Space → Euclid Space
→ Hilbert Space
从信号处理的角度理解,在小波变换中,信号可通过信号滤波器分解为高频分量(高频子带)和低频分量(低频子带),高频子带又称为细节(detailed)子带,低频子带又称为近似(approximate)子带。细节子带是由输入信号通过高通滤波器后再进行下采样得到的,近似子带是由输入信号通过低通滤波器后再进行下采样得到的。
小波变换的内容很多,一下两下真的说不清楚(想说清楚我也看不懂),但基本原理就是这些。随着应用的深入在做学习比较靠谱。
二进小波变换(DWT)
在小波变换中,若对尺度按幂级数作离散化,同时对平移保持连续变化,则此类小波变换称为二进小波变换(Dyadic Wavelet Transform)。
紧支撑小波基
在小波变换中,紧支撑小波基是性质较好的一类小波基,紧支撑(Compact Support)函数是指这样的一类函数:其自变量仅在0附近的取值范围内能得到非零函数值,而在其他区间取值,则得到的函数值全为零。能得到非零函数值的自变量取值区间被称为该函数的支撑区间。
一个函数的支撑区间长度主要由其尺度参数决定。支撑区间越大,计算复杂度越高,边界拖尾效应越明显。不仅如此,支撑区间越大,会产生更多的高幅值小波系数,关于这个结论的解释,可参考傅里叶变换使用无限长(支撑区间大)的三角函数基进行信号拟合的情况,相比于使用信号迅速衰减(支撑区间小)的小波基,三角函数基拟合信号时需要更多的数量。因此在选择小波基时,以支撑长度较短的小波基为宜。
此外,小波基的正交性也是一类重要的性质,它确保了信号的分解没有冗余(最优分解)。
小波包变换(WPT)
小波变换的缺陷
同上,小波变换仍存在着不足之处,由于正交小波变换只对信号的低频部分做进一步分解,而对高频部分也即信号的细节部分不再继续分解,所以小波变换能够很好地表征一大类以低频信息为主要成分的信号,但它不能很好地分解和表示包含大量细节信息(细小边缘或纹理)的信号,如非平稳机械振动信号、遥感图象、地震信号和生物医学信号等。
原理
小波包分解(Wavelet Packet Decomposition),又称为最优子带树结构(Optimal Subband Tree Structuring)是对小波变换的进一步优化。
主要思想:在小波变换的基础上,在每一级信号分解时,除了对低频子带进行进一步分解,也对高频子带进行进一步分解。最后通过最小化一个代价函数,计算出最优的信号分解路径,并以此分解路径对原始信号进行分解。
小波包变换可以对高频部分提供更精细的分解,而且这种分解既无冗余,也无疏漏,所以对包含大量中、高频信息的信号能够进行更好的时频局部化分析。
从函数理论的角度来看,小波包分解是将信号投影到小波包基函数张成的空间中。从信号处理的角度来看,它是让信号通过一系列中心频率不同但带宽相同的滤波器。
小波函数基
无论是小波变换还是小波包变化,一个重要的环节是选择合适的小波函数基进行信号分解。
在选择合适的小波函数基时,需要考虑的因素
小波的对称性:主要体现在保证信号重构时不会产生相位畸变,即是不会产生重构信号的相位失真。
小波的正则性:保证了信号的光滑和可微性,对于大部分小波而言(非全部),其与消失矩存在关系:小波的消失矩越大,正则性也就越大。
选择与输入信号的波形相似性高的小波:意义在于使数据压缩和降噪变得更容易(信号的拟合和分解都更容易)。
几种常用的小波函数基:
Haar小波
最简单的一个小波函数,其具有紧支撑性和正交性,函数图像为在支撑区间[0,1)上的单个矩形波。Haar小波在时域上不连续,作为基本小波时性能不是很好。
