原创文章,转载、引用请注明出处!
感谢WCX、DHF等在本文写作中给出的建议。
PolyFit: Perception-Aligned Vectorization of Raster Clip-Art via Intermediate Polygonal Fitting
通过中间多边形拟合实现光栅剪贴画的感知对齐矢量化
来自SIGGRAPH 2020的一篇文章,做的是光栅图像矢量化。
立意
clip-art images是什么?为什么可以做矢量化?为什么要做矢量化?本篇的核心是什么?
Clip-art images,中文译为剪贴画,通常用于数字媒体中。
光栅剪贴画图像由明显的彩色区域组成,这些区域由清晰的边界隔开,通常允许清晰的心理向量解释。
Raster clip-art images, which consist of distinctly colored regions separated by sharp boundaries typically allow for a clear mental vector interpretation.
目前,由于各种原因,大量的剪贴画图像仍然以光栅格式创建和存储。但实际上,剪贴画图像可以以矢量形式紧凑无损地表示。图形矢量化后,在对图形进行调整大小等方面的操作时就会极大的提高效率和提升用户体验。这也是光栅图像矢量化算法开发的最直接驱动,即现代媒体的商业用途。
Clip-art images can be compactly and losslessly represented in vector form; yet, for a variety of reasons, large numbers of clip-art images are still created and stored in raster format…… Vectorizing these images would enable resolution-free reuse of artwork created for legacy displays and facilitate a range of operations such as resizing or editing, which are easier to perform on vector rather than raster data. Vectorizing this data in a man- ner consistent with viewer expectations poses unique challenges, motivating the development of algorithms specifically designed for clip-art vectorization
虽然先前的方法成功地将光栅剪贴画分割成符合观众期望的区域,但在满足观察者期望的同时,将这些区域之间的光栅边界矢量化仍然是一项挑战:现有的算法仍然经常无法产生与人类偏好一致的向量边界(图1b-c,2b-d)。我们提出了一种在光栅剪贴画图像中实现区域边界矢量化的新方法,该方法明显优于这些早期方法,产生的结果更符合观众的期望(图1e、2e)。
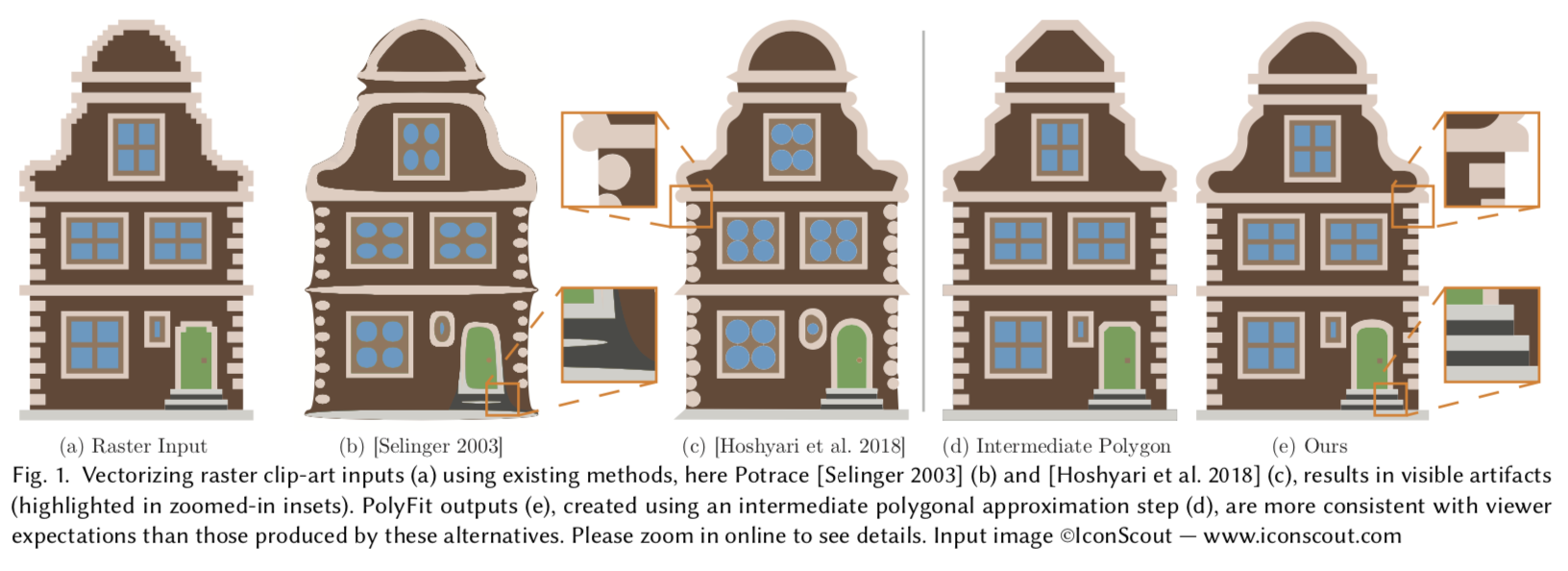
Notably, while prior methods [Kopf and Lischinski 2011] successfully segment raster clip-art into regions consistent with viewer expectations, vectorizing the raster boundaries between these regions while meeting observer expectations remains challenging; existing algorithms still often fail to produce vector boundaries consistent with human preferences (Figures 1b-c, 2b-d). We present a new approach for vectorization of region boundaries in raster clip-art images that significantly outperforms these earlier approaches, producing results much better aligned with viewer expectations (Figures 1e, 2e).
基于上述情况,这篇文章提出了PolyFit,可以产生与人类偏好相一致的矢量化图像。
方法
带有人类主观偏向的矢量化过程的评价标准
Sec. 3
本文的思路更偏向人的主观意愿去做矢量化(本来就是做给人看的,主观评价很重要),所以文章先叙述了带有人类主观偏向的矢量化过程的评价标准:2018H;Koffka 1955;Wagemans 等人,2012,确定的可能影响人类心理矢量化过程的主要标准有:准确性、简单性、规则性和连续性。
accuracy, simplicity, regularity, and continuity
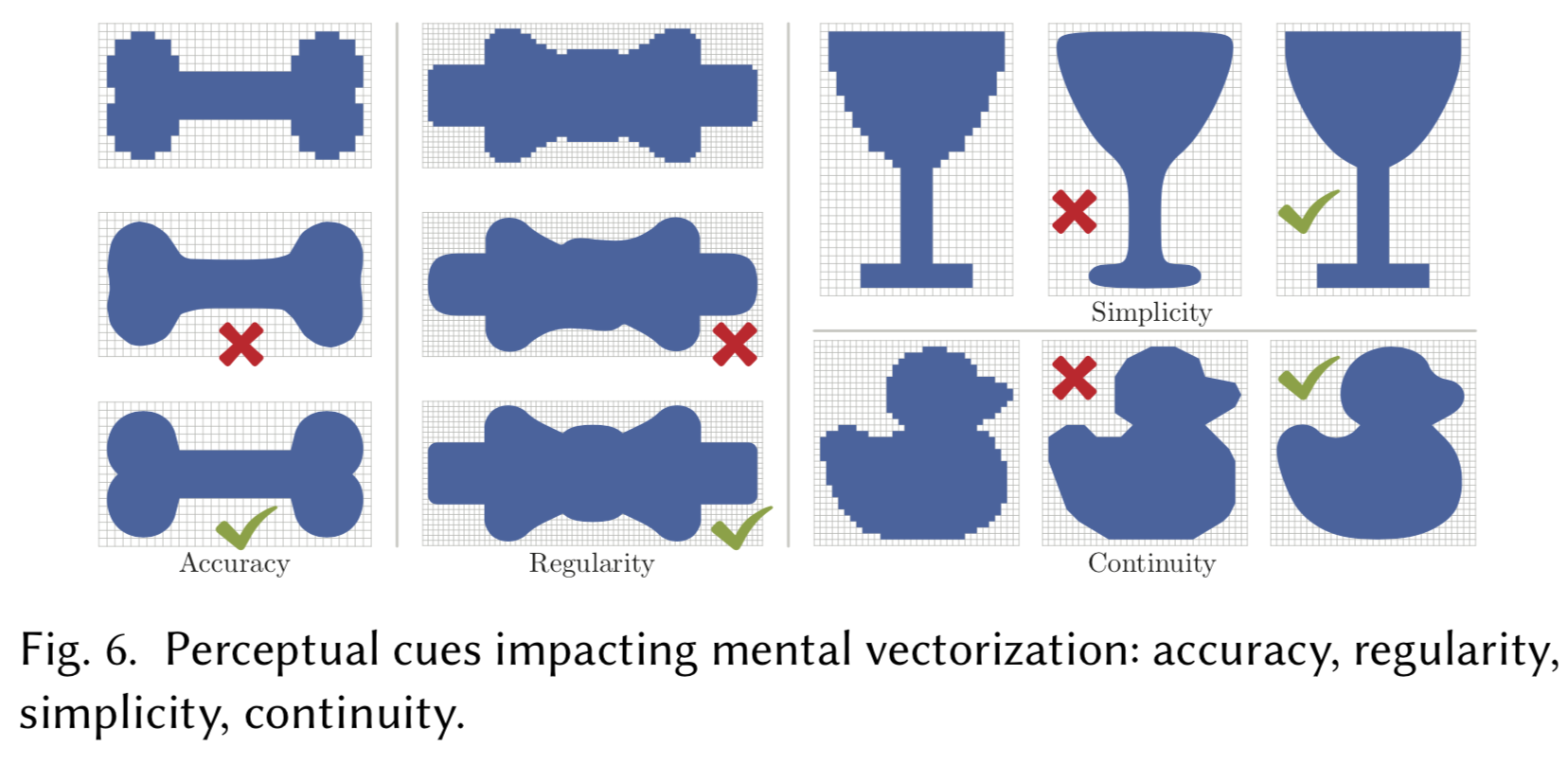
准确性:预示着人类所设想的矢量化在几何上接近输入栅格边界。
简单性:主张输出由最少数量的几何基元组成,主张优先考虑直线而不是曲线,主张优先选择曲率变化较小的曲线。
规则性:观察者希望更观察到的精确或近似的规律性,如栅格输入中存在的平行性、对称性。
连续性:观察者倾向于将栅格区域边界“臆想”为片状连续曲线。
方法概述
Sec. 3
该方法的输入是光栅剪贴画图像,这些图像都具有一个特征:由许多具有清晰可辨的区域间边界的独特颜色区域组成。
整个方法可分为两部分:首先使用[Kopf 和 Lischinski 2011]的框架将光栅图像分割成单色区域。然后将所得区域之间的栅格或片状轴对齐的边界转换为符合观众感知的片状平滑曲线。
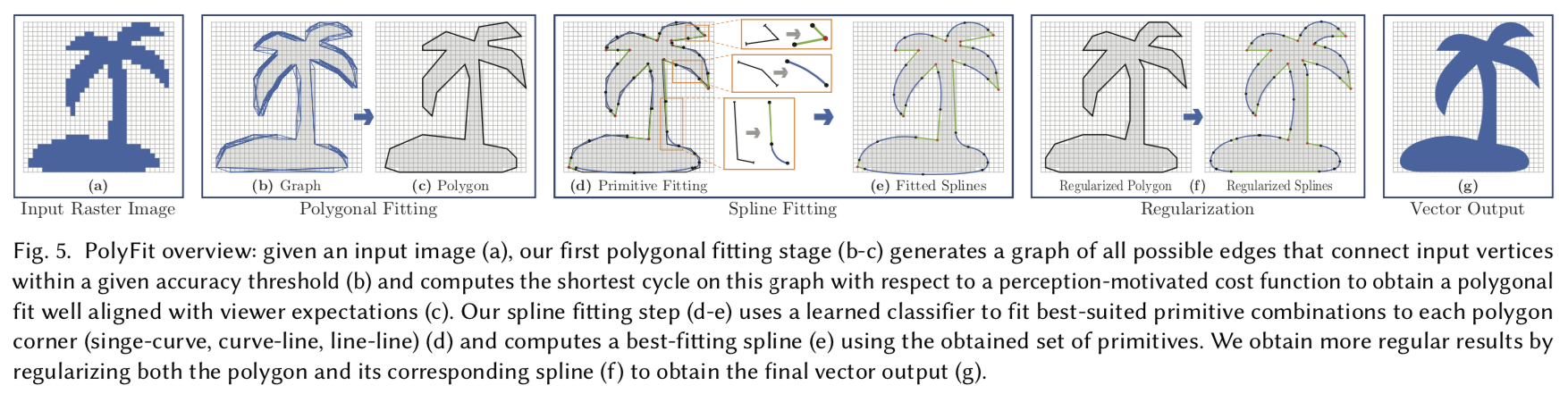
给定输入图像(a),我们的第一个多边形拟合阶段(b-c)生成一个在给定精度阈值(b)内连接输入顶点的所有可能边缘的图,并计算该图上相对于感知激励成本函数的最短周期,以获得与观察者期望完全一致的多边形拟合(c)。我们的样条拟合(spline fitting)步骤(d-e)使用学习的分类器将最适合的基元组合拟合到每个多边形角(简单曲线、曲线-直线、直线-直线)(d),并使用获得的基元集计算一个最适合的样条(e)。我们通过对多边形及其对应的样条(f)进行正则化,以获得最终的向量输出(g),从而获得更规则的结果。
上图的d-e、f是本文的核心内容,即边界的转化工作。
中间多边形近似
问题定义
文章将中间多边形近似的问题表述为:寻找一个环(cycle),该环是最小化定义在有向图G=(V,E)中的成对和三对边上(pairs and triplets of edges)的能量函数(energy function)。
We formulate the extraction of an intermediate polygonal approximation as the problem of finding a cycle that minimizes an energy function defined on pairs and triplets of edges in a directed graph G = (V,E),wheretheverticesV representcandidatecornersandthe edges E represent candidate polygon segments (see Fig. 5b).
为了方便高效的计算,原文通过只包括“有合理可能成为最终多边形一部分的顶点和边”来保持被操作图的小尺寸。然后,通过图的构造,以平衡准确性、简单性和连续性为标准计算在这个图上的最优周期。
最终,寻找在成对和三倍边上的能量函数的最优周期问题简化为一个经典的最短周期问题。
and continuity (Sec. 4.2, Fig. 5c) via a graph construction that reduces the problem of finding the optimal cycle of an energy function defined on pairs and triplets of edges to a classical shortest-cycle problem.
图形结构
使用想塑角到边缘的曼哈顿距离来定义大致的形状:丢弃所有违反曼哈顿距离标准的边缘,并要求所有错误分类的像素都位于直线的一侧,丢弃不满足这一属性的边缘。
简言之,这部分工作的目的是:给定大致范围
多边形近似
在评估多边形的最优性时,根据第3节中确定的三个感知标准(准确性、简单性和连续性)来评估。
准确性
使用之前计算出的错分像素集Pij来衡量每个边缘相对于栅格边界的准确性。
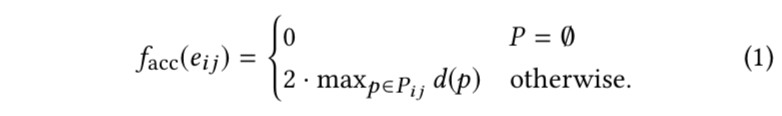
连续性
用多边形角上的角Aijk=eijejk作为连续性的离散代表。Aijk是角处的内外角中较小的角。
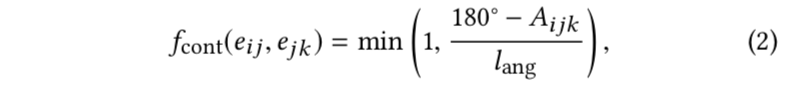
简单性
将简单性表达为对最小曲率变化和较小多边形边缘数的偏好。
以连续角度之间的相似性来衡量曲率变化。
为了最大限度地减少拐点的出现(与幅度无关),为每个拐点边缘增加一个绝对拐点惩罚,即binfl=0.1,并使用两个角度中较小的一个(较尖锐的一个)来评估拐点的幅度。这个幅度的饱和极限设置为linfl=90°。
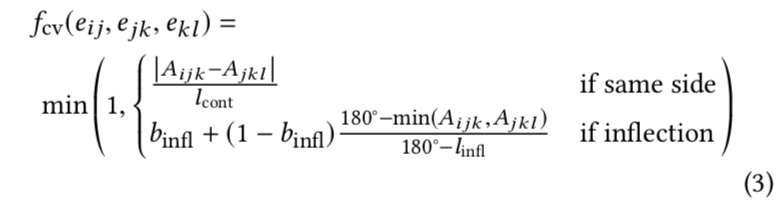
简单性也主张减少多边形边的数量。为此,我们给所有图边缘分配一个小的惩罚ε=1e-3,并进一步惩罚冗余的像素长边缘。

综合多边形成本
综合多边形成本C(P)是上述项在所有边和连续边的对和三倍体上的总和。
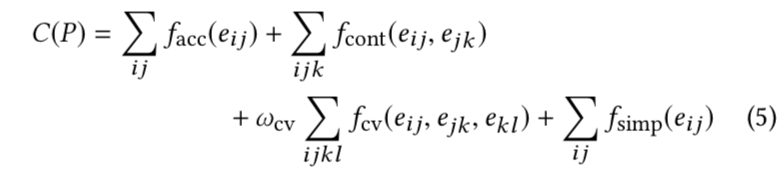
样条拟合
Sec. 5
算法的第二步是将封闭地、片状光滑地样条拟合到多边形上。
计算这种拟合需要求解几组变量,分别是:
定义样条地基元序列(由其类型定义);
基元与其拟合地栅格边界段之间地映射(特别是基元断点和栅格边界位置之间地对应关系);
基元地形状参数(控制点的位置)。
样条基元
根据以下设定:
多边形和样条都要准确地近似于输入的栅格,中间多边形边缘的切线要与最终样条的切线密切相关;
希望样条将通过接近多边形边缘中点,并且在这些中点附近的样条切线与边缘切线相似
希望角样条部分至少和它们匹配的多边形角一样连续(即最多有一个C0不连续),并期望它们尊重多边形角所施加的基元数的上界(即两个)。
确定了三种角跨基元配置,它们反映了简单性和连续性之间所有不同的平衡选择。
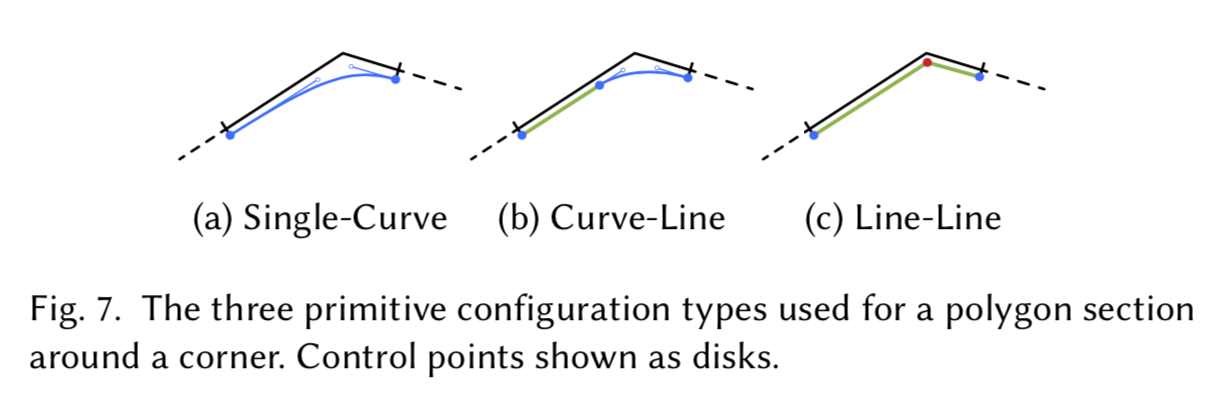
总体目标是产生一个最佳平衡平滑性、简单性和输入栅格的准确性的养条。为了找到这样的养条,在分类过程中,使用优先考虑连续性来考虑配置类型。
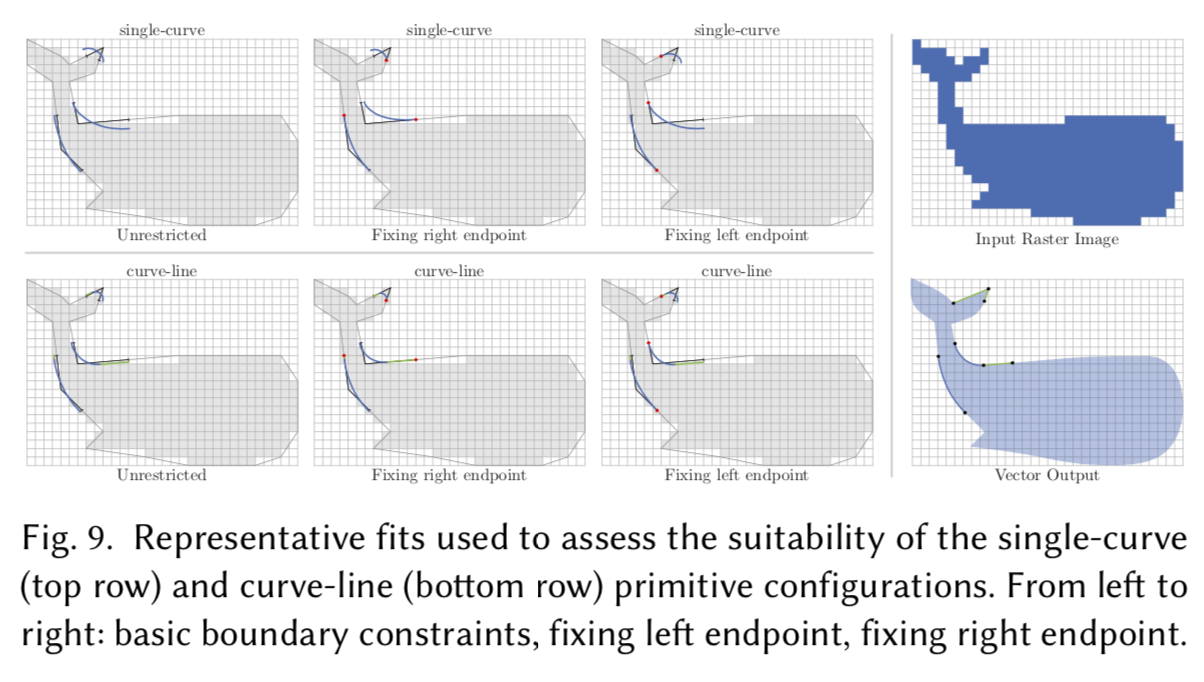
训练和验证
对拥有100棵树的森林进行了训练,在23张不同分辨率的输入图像上手工标注多边形角,显示出各种各样的几何构型。50%用于训练,50%用于测试,在测试数据集上达到了99.3%的准确率。
二元决策使用的是置信度,阈值是0.75。
规范化
Sec. 6
因为前面提到过,人类观察者能够识别输入数据中的规律性,并期望在拟合或矢量化过程中保留这些规律性,所以,这部分工作的目的是在最终输出中保留输入的正则性,关注的是对称性、平行性、连续性和轴对齐。
正交和轴对齐的边:通过不允许对两个入射多边形角使用(单一)曲线基元配置(从而迫使方法沿这些边缘使用曲线线或线型配置),使长度至少为各自边界框边范围50%的轴对齐边缘更加突出。
平行边缘:检测并强制执行存在于栅格输入中的突出的轴对齐平行边缘:如果边缘之间的距离不超过它们的重叠长度,才认为这些边缘是突出的。
对称性:如果两个栅格对称性发生冲突,会优先考虑非规则化多边形中先验存在的对称性,并优先考虑较长的对称边界路径。
(曲线)延续:在光栅层面(轴对齐)和多边形层面(任意方向)都检测并强制执行连续。
多色输入
Sec. 7
上面叙述的都是一个由两个颜色均匀的区域组成的图像的情况。但现实生活中,图像通常包含多个彩色区域。

对于这种输入,处理方法是:将两个相邻的区域都将其交界处分类为平滑配置,只有当分别对区域进行矢量化会产生一个以交界处为顶点的平滑配置类型的多边形,如果不是这种情况,最多只允许两个相邻区域中的一个区域被分类为光滑配置。
实验结果
Sec. 8
与以往结果的对比
文章将其结果与2018H等最近两个排名最高的方法在81个输入(Potrace[Selinger 2003]以及2018H)上产生的结果进行了比较。测试数据集包括37个单一区域边界的输入,28个低分辨率多色输入,以及16个中高分辨率的多色输入。对所有方法都使用默认参数。

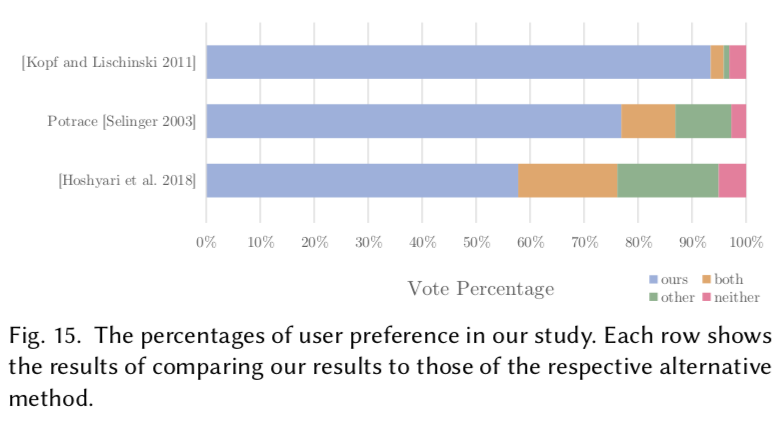
该部分实验主要着眼在区域分辨率为100以下的输入。对于较高的分辨率,拟合精度对于最终结果起决定性作用,所有方法产生的结果都相当相似。但在较低的分辨率下(16×及以下),原文方法有着明显的优势,并且在94%的情况下优于2018H的结果。
与手动矢量化的对比
文章将其结果与艺术家进行的手动矢量化结果进行了对比。因为手动矢量化多色输入非常耗时(一个区域需要 30多分钟才能准确拟合),所以这部分只针对2018H提供的15张矢量化二元图像进行了试验。
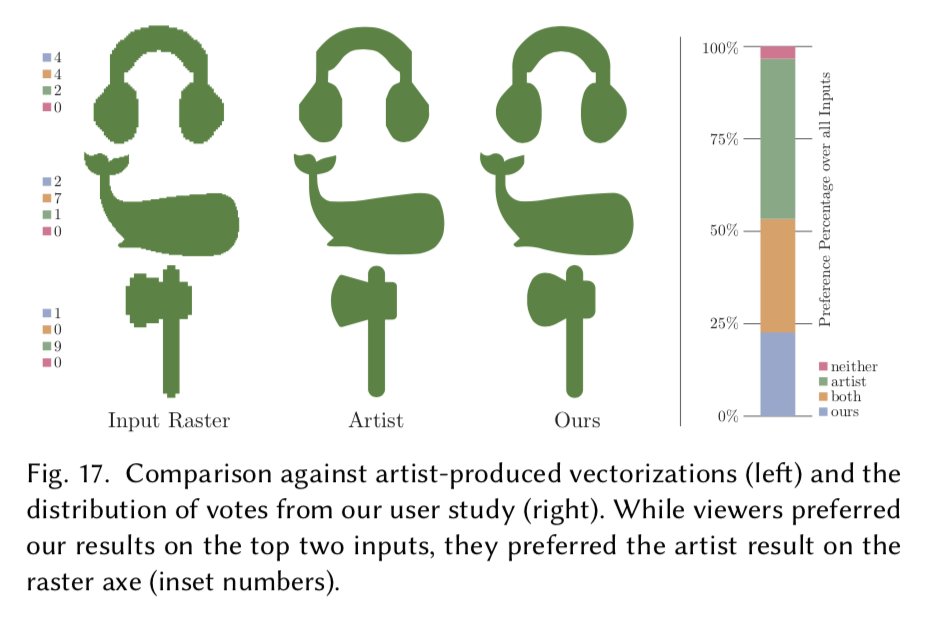
在55%的结果中,参与者认为本文方法得出的结果比艺术家给出的结果更好。
当艺术家的结果被认为是更好的输入时(如图17c),猜测是由于识别–因为艺术家的输出反映了作者对所绘形状的知识。
总结
本文给出了PolyFit这种新的剪贴画矢量化方法,并给出了与现有的替代方法相比的结果。
优点
能产生更符合观察者意愿的结果(文章的核心立意的努力方向)。
在低分辨率数据上表现得特别好(结果提到了16×、32×和64×)。
性能
Sec. 8
对于分辨率为32×和64×的单个区域,该方法分别需要0.5秒和1.2秒(中位数)来完成矢量化。大部分的运行时间是分布在初始花键拟合和后续的角反馈循环之间的时间大致相等。多边形取阶段平均占总运行时间的 10%到20%,并且随着输入中存在更多的正则性而增加,这就需要对多边形进行更多的正则化工作。
上述时间是在八代英特尔酷睿 i7、3.7GHz主频CPU下进行的实验结果。远快于2018H的时间(后者平均需要30到50倍的时间)。
局限
Sec. 8
该方法目前的实现只对单个边界进行规范化。在许多情况下,它默认实现了边界间的平行性。对这种平行性的明确检测和执行将是我们方法的一个重要的实际扩展。
Our current implementation only regularizes individual boundaries. It achieves inter-boundary parallelism by default for many cases. Explicit detection and enforcement of such parallelism would be an important practical extension of our method. In the future, one can similarly extend our regularization step to address regularities between regions, e.g., using continuation detection, complementing our core method.
相关工作
本文的研究建立在样本点的逼近、笔触美化、自然图像矢量化、艺术家生成的图像矢量化这几个领域和解决剪贴画矢量化的一些商业软件包的基础上。其中本文主要引用了Hoshyari等在2018年发表的Perception-Driven Semi-Structured Boundary Vectorization,本文工作是在该文的基础上做的改进。此外,本文使用的中间多边形拟合方法受到Potrace[Selinger 2003]启发,在其基础上约束多边形以准确地保存输入细节,有更准确的最终拟合。
Perception-Driven Semi-Structured Boundary Vectorization
ACM Transaction on Graphics 37, 4 (2018)
https: //doi.org/10.1145/3197517.3201312
这篇文章针对艺术家生成的光栅输入的可操作的矢量化算法。给出了一种算法,能够通过将学习到的分类器预测与关于角认知的见解相结合,从有限的训练数据中获得感知上一致的角分类。方法步骤如下:
模型学习:使用随机森林从带有人工标注的角的训练栅格图像集合中学习推理局部的几何环境,并使用一个训练好的分类器计算局部角概率。
模型整合:将数据驱动的模型预测与后续的基于感知的角处理步骤相结合,逐渐修剪模型输出的角集,直到使用得到的角计算的边界矢量化符合标准。
模型优化:框架定位角的同时,并在它们之间拟合简单的G1连续样条曲线。角集最终确定后,继续进一步简化输出。
框架包括三个主要步骤:(a)潜在角检测、(b)迭代角去除、(c)全局正则化。颜色区分不同的曲线类型。

Potrace: a polygon-based tracing algorithm
将位图转换为矢量轮廓图,这种逆向过程称为跟踪。
这篇文章描述了一个简单,有效的跟踪算法:Potrace。该算法输出是由Bezier曲线构成的光滑轮廓,它使用多边形作为图像的中间表示。
路径分解:位图被分解成许多路径,这些路径形成了黑白区域之间的边界。
最优多边形生成:用最优多边形逼近每条路径。
光滑轮廓:将每个多边形转化为光滑的轮廓。
曲线优化(可选):通过在可能的地方连接连续的Bezier曲线片段来优化生成的曲线。
输出:以所需的格式生成输出。
一个完整的示例:(a)原始位图;(b)路径分解和最优多边形;(c)顶点调整、角点分析和平滑;(d)曲线优化;(e)最终输出。

其他
光栅图像与矢量图像
所有的电子艺术图像可被分为两种核心类型:光栅图像和矢量图像。
简言之,光栅图像由像素点组成,矢量是由连接的线组成的图像。
光栅图像
特征
光栅图也称为位图、点阵图、像素图。
简言之,最小单位由像素构成的图,就被称为光栅图像。在光栅图像中,只包含像素点的信息,每个像素点有自己的颜色。
光栅图形最为人知晓的特征,就是它在放大时会失真。
这种格式的图适合存储图形不规则,而且颜色丰富没有规律的图,比如照相,扫描等。
分辨率
光栅图像或扫描图像的分辨率以DPI(Dots Per Inch,每英寸点数)表示。
DPI原来是印刷上的记量单位,意思是每英寸上,所能印刷的网点数(Dot Per Inch)。但随着数字输入,输出设备快速发展,大多数的人也将数字影像的解析度用DPI表示。
但较为严谨的情形下,印刷时计算的网点(Dot)和电脑显示器的显示像素(Pixel)并非相同,所以较专业的人士,会用PPI(Pixel Per Inch)表示数字影像的解析度,以区分二者。
文件
为了准确地记录光栅图像文件,图形软件必须跟踪大量信息,包括像素点集中每个像素的确切位置和颜色。这就导致光栅图像的文件很大。高DPI和更大的颜色深度也会产生更大的文件大小。典型的“2X3” 150 dpi黑白光栅图像徽标的文件大约为70K。保存为300 dpi 24位(百万种颜色)光栅图像文件时,大小可能会超过100倍。
常见的光栅图像格式包括BMP(Windows位图),PCX(画笔),TIFF(标签交错格式),JPEG(联合图像专家组),GIF(图形交换格式),PNG(便携式网络图形),PSD(Adobe PhotoShop)和CPT(Corel PhotoPAINT)。
矢量图像
特征
矢量图像是生成对象的连接线和曲线的集合。在矢量插图程序中创建矢量图像时,会插入节点或绘图点,并且线条和曲线将注释连接在一起。这与“连接点”的原理相同。
分辨率
矢量图像的分辨率由数学定义(不是像素),所以它们可以按比例放大或缩小而不会失真。当插图(绘图)程序向上或向下调整矢量图像的大小时,它只是将对象的数学描述乘以缩放因子。这也是矢量图形在剪贴画中特别受欢迎的一个重要原因。
文件
矢量图像不需要跟踪图像中的每个像素,只需要数学描述。因此,矢量文件的文件大小非常小。矢量文件的主要内容就是数学的描述。所以,矢量文件非常适合通过网络传输。
常见的矢量格式包括EPS(Encapsulated PostScript),WMF(Windows图元文件),AI(Adobe Illustrator),CDR(CorelDraw),DXF(AutoCAD),SVG(可缩放矢量图形)和PLT(Hewlett Packard图形语言图文件)。
曼哈顿距离
曼哈顿距离为:在平面直角坐标系中,两点在坐标轴方向上的距离之和,即d(i,j)=|xi-xj|+|yi-yj|。
对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此,曼哈顿距离又称为出租车距离。
曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同。
曼哈顿距离示意图在早期的计算机图形学中,屏幕是由像素构成,是整数,点的坐标也一般是整数,原因是浮点运算很昂贵,很慢而且有误差,如果直接使用欧氏距离(欧几里德距离:在二维和三维空间中的欧氏距离的就是两点之间的距离),则必须要进行浮点运算,如果使用曼哈顿距离,则只要计算加减法即可,这就大大提高了运算速度,而且不管累计运算多少次,都不会有误差。
多边形拟合
这是一个专门的研究方向。不管是已有的进行多边形拟合的轮子还是使用多边形拟合做的图形学研究,都有这个概念。
opencv里有多边形拟合的函数approxPolyDP,natlab里有名为polyfit的函数等。
所介绍的这篇论文使用了这个概念去做矢量化。
