原创文章,转载、引用请注明出处!
AdderNet
AdderNet: Do We Really Need Multiplications in Deep Learning?
CVPR 2019
立意
在深度学习算法中,卷积操作被广泛的用于度量输入特征和卷积滤波器之间的相似性。
GPU+深度卷积神经网络,大大加快了计算机视觉领域的发展。但GPU有着显而易见的缺陷,主要是物理因素所导致的。第一个是功耗问题,再一个是体积问题。这两个问题导致了现有的多数深度学习方法只能运行在装有大型GPU的机器上。人们希望这些算法能在小巧的移动设备上实现。因此,目的就是降低算法的运行成本,使得在硬件配置不够的情况下也能高效的运行这些深度算法。
在正向推理过程中,深层神经网络的计算大多是浮值权和浮值激活的乘法运算。显然,乘法运算比加法运算要慢。
本文提出的AdderNet,就是在放弃卷积运算的同时,利用l1距离,最大限度地描述和利用加法,逼近卷积操作的精度。为了保证模板的充分更新和网络的收敛性,设计了一种改进的梯度正则化反向传播算法。
数学描述
Adder Network
对于CNN中的卷积运算,假定输入特征X,filter表示为F,卷积后输出的是二者的相似性度量,表述如下面公式:
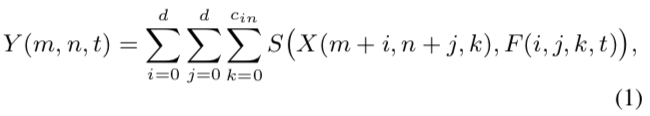
其中,d为kernel size,c_in和c_out分别为输入、输出通道数;卷积核F的大小则为d × d × c_in × c_out;H和W为输入特征的长和宽,输入特征X的大小为H × W × c_in。
以及,S(·,·)是相似性度量,也就是距离度量函数。如果将互相关(cross-correlation)作为距离的度量,即S(x,y)= x × y,这时式(1)成为卷积运算。式(1)还可以表示当d=1时计算完全连接的层。
还有许多其他度量来测量滤波器和输入特征之间的距离,但这些度量大多涉及乘法。
于是,希望在式(1)中用加法来代替乘法。L1距离仅涉及到两个向量差的绝对值,不包含乘法。因此,通过计算滤波器和输入特征之间的L1距离,式(1)可以重新表示为:
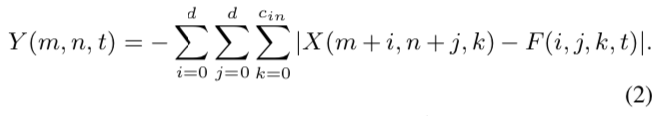
不论是使用互相关,还是L1距离,都可以完成相似性度量,但二者的输出结果还是有一些差别的:通过卷积核完成输入特征图谱的加权和计算,结果可正可负;但adder filter输出的结果恒为负,为此作者引入了batch normalization将结果归一化到一定范围区间内,从而保证传统CNN使用的激活函数在此依旧可以正常使用。
用式(3)计算的特征都是负数,因此在特征计算后,采用BN层来归一化,之后再用激活函数提高特征非线性。
Optimization
神经网络利用反向传播来计算滤波器的梯度和随机梯度下降来更新参数。
在CNN中,输出特征Y相对于滤波器F的偏导数被计算为:
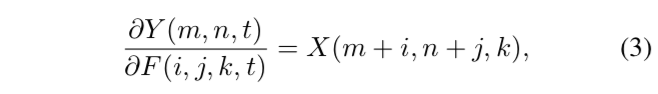
在AdderNets中,Y相对于F的偏导数是:
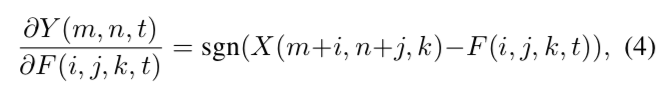
sgn(·)是阶跃函数,取-1、0、1。
式(4)中等号右边的是signSGD,signSGD被证明的缺陷是几乎不会选择到最陡的方向,而且随着维度增加效果会更差。
因此AdderNet使用如下公式进行梯度更新:
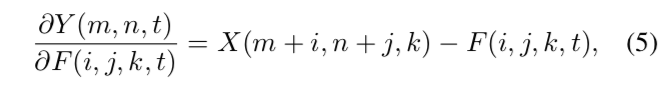
此外,如果使用全精度梯度的更新方法,由于涉及到前层的梯度值,很容易导致梯度爆炸。这里使用HardTanh将输出限定在[-1,1]范围内:
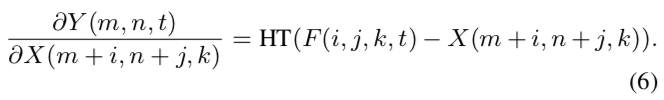
梯度计算也好了,接下来的问题是:加法层的方差会很大。
Adaptive Learning Rate Scaling
在传统的CNN中,假设权值和输入特征是独立的,服从正态分布,输出的方差大致可以估计为:
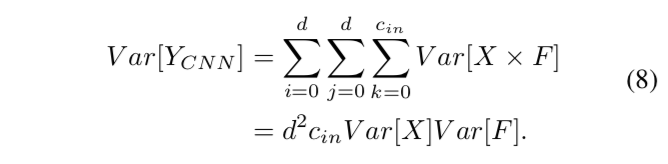
对于AdderNet,输出的方差可以近似为:

实际上,权重var[F]的方差通常非常小(10^−3~10^-4)。因此,式(9)中的加法运算会比式(8)带来更大的输出方差。
式(8):var[X] × var[F]
式(9):var[X] + var[F]
AdderNet的输出具有较大方差,在更新时根据常规的链式法则会导致梯度比常规CNN更小,从而导致参数更新过慢。
这里,最容易想到的解决方法就是:使用大的learning rate。这样虽然可以提高学习速度,但是文中又指出,不同层其权重梯度变化很大:
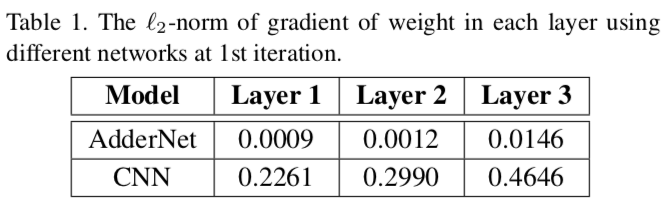
这表明每一层的参数需要不同。因此作者给每一个adder layer设计了不同学习率:
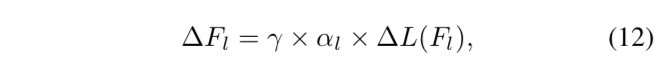
其中,γ是整个神经网络的全局学习速率,∆L(Fl)是层L中过滤器的梯度,αl是其相应的局部学习率。
输入是经过BN的,也就是说在AdderNet中,filters的值也是经过了归一化。
局部学习率αl定义为:
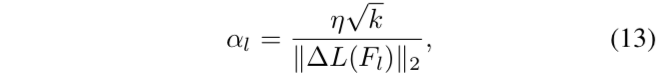
其中,η是一个控制adder filters学习率的超参数,k是Fl中参数的个数。
Adder Network的前馈和反传流程

实验
实验环境
NVIDIA Tesla V100 GPU:2017年中发布、16/32GB(文中没提用的是什么显存的版本)
PyTorch
MINST + LeNet-5-BN + AddNN/CNN
结果:
CNN的准确率为99.4%∼435K乘法。
通过将卷积运算中的乘法替换为加法运算,该加法网的准确率达到99.4%∼870K加法,几乎没有乘法。
训练设置:
- 图像大小:调整为32×32;
- 优化:Nesterov加速梯度法(NAG);
- weight decay/momentum:5×10^−4/0.9;
- 初始lr为0.1、cosine learning rate decay(余弦学习率衰减);
- 用加法器滤波器代替LeNet-5-BN中的卷积滤波器、将全连接层中的乘法替换为减法;
- 50个epochs的训练。
CIFAR-10/100 + VGG/ResNet + BNN/AddNN/CNN
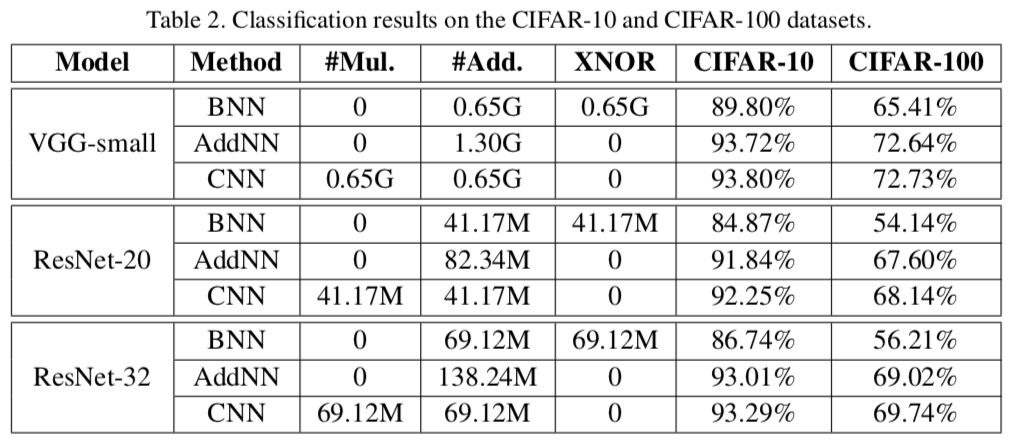
结果:
对于VGG,AddNN与CNNs(CIFAR-10为93.80%,CIFAR-100为72.73%)的结果基本相同(CIFAR-10为93.72%,CIFAR-100为72.64%);BNN的模型尺寸比AdderNet和CNN小得多,精度也低得多(CIFAR-10为89.80%,CIFAR-100为65.41%);
对于ResNet-20,CNNs的精确度最高(CIFAR10为92.25%,CIFAR-100为68.14%),但乘法次数较多(41.17M),AddNN少了0.5个点左右(CIFAR-10和CIFAR-100中的无乘法运算精度分别为91.84%和67.60%)。
由于二进制神经网络BNN可以使用XNOR运算来代替乘法,所以还比较了BNN的结果。
XNOR:同或。(1 XNOR 1 = 0 XNOR 0 = 1,1 XNOR 0 = 0 XNOR 1 = 0)
训练设置:
- 图像大小:32×32;
- 与何凯明大佬2016年残差那篇相同的DA和处理方法;
- 初始lr为0.1、后续遵循多项式学习率时间表;
- bs=256;
- BNN中,将第一层和最后一层设置为全精度卷积层;
- 400个epochs的训练。
ImageNet + ResNet + BNN/AddNN/CNN
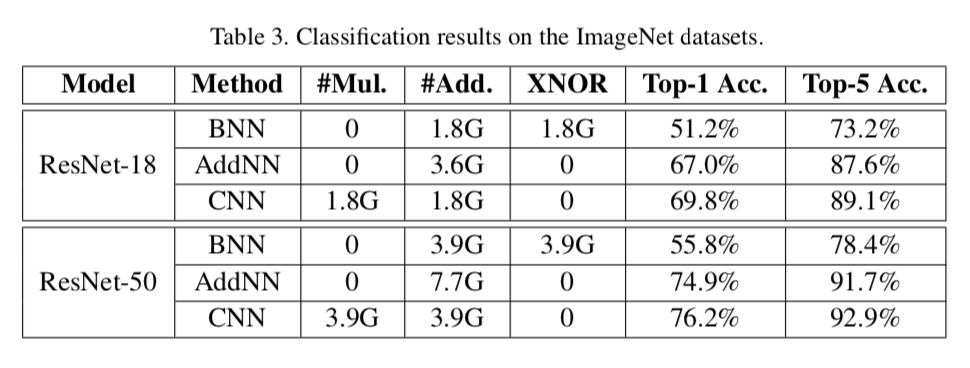
其它
感想
首先,文章思路很不错。相似的思路之前也提过,这一篇的内容做的挺多的,不管是数学方面的论证还是实验部分做的都还不错,比较清晰。
以及看了知乎上这篇文章的团队内成员的答复和一些网友的评论,整体的评价也还不错,去年6月份的时候,大部分都还在求硬件加速之类的,官方也说会给出预训练模型,接下来的一篇文章也是继承了这个工作,说明这个工作持续的在做。这是比较nice的。
缺陷也有,最主要的一点就是为什么最后的实验不去对比GPU下的速度?显得有点文不对题,故意隐瞒,不是特别的convincing。以及实验主要做的是图像分类的问题,但也没提修改了卷积操作之后,在别的领域的应用,也没特别说明只是针对图像分类问题做的。
最后,有一点没看懂,就是做的是简化网络,从GPU转移到CPU,但是最终部署的时候用的还是GPU,且没给CPU的主频信息等,包括文章中没有特别提到的硬件方面的东西,包括cuda编程等。这些都是没说清楚的点,也许不重要?但是这要不说清楚,代码都不怎么看得懂,哪有心思跑它。
AdderSR
AdderSR: Towards Energy Efficient Image Super-Resolution
CVPR 2021
立意
AdderNet用于SISR问题中会出现两个问题:
加法器不能很容易的学习身份映射(identity mapping);
加法器不能实现高通滤波。
Specifically, the adder operation cannot easily learn the identity mapping, which is essential for image processing tasks. In addition, the functionality of high-pass filters cannot be ensured by AdderNets.
换言之,在SISR中,AdderNet需要保证两个重要特性:各卷积层输入输出特征的相似性和高频信息的细节增强。
In SISR, there are two important properties that should be ensured by adder neural networks: the similarity between the input and output features of each convolutional layer, and the enhancement of details w.r.t. high frequency information.
VDSR中输入图像“蝴蝶”的不同层的输出特征映射。任何两个相邻层之间的差异在纹理和颜色信息上都非常相似。高频信息的细节随着深度的增加而增强。这两个重要性质需要加法神经网络来保证。
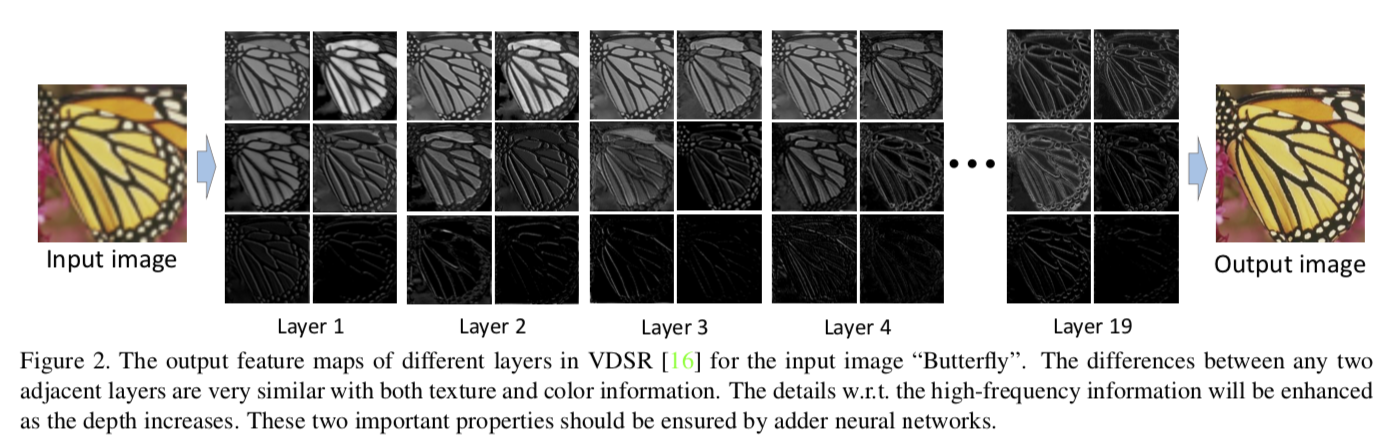
这篇文章分别设计了模块去解决了上述问题,最终使AdderNet的SISR模型逼近CNN性能。
To maximally excavate the potential for exploiting AdderNets to establish SISR models, we first analyze the theoretical difficulties for applying the additions into SISR tasks. Specifically, input and output features in any two neighbor layers in SISR models are very close with the similar global texture and color information as shown in Figure 2. However, the identify mapping cannot be learned by a one-layer adder network. Thus, we suggest to insert self-shortcuts and formulate new adder models for the SISR task. Moreover, we find that the high-pass filter is also hard to approximate by adder units. We then develop a learnable power activation. By exploiting these two techniques, we replace the conventional convolution filters in modern SISR networks by adder filters and establish AdderSR models accordingly.
数学描述
背景
一般的SISR任务的目标函数可以表示为:
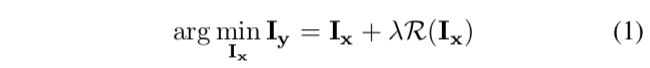
其中,其中Iy是观测数据,即低分,Ix是期望的高分辨率图像,R(·)表示所使用的先验信息,例如平滑和加性噪声,λ是权重。
式(2)又提了一遍加法器模型,就是上一篇的式(2)。
本篇的式(2)跟上一篇的式(2)有一点点不一样,就是求和号的角标都是从1开始的,上一篇是从0;以及换了两个字母表示。不过应该不是什么问题。
Learning Identity Mapping using AdderNet
一上来,这个恒等映射的作用就没太看懂,查只能查到何大佬那篇文章,但也没有引,公式是一模一样的,不知道说的是不是一个事情。
图2表明,在使用深度学习方法的SISR任务中,恒等映射Iy=F(Iy)是非常必要的。
对于传统的卷积网络,当权值为单位矩阵时,恒等映射很容易学习。但AdderNet使用的是l1范数,虽然l1距离可以很好地完成图像分类任务,但是不能逼近恒等映射。
使用多个Adder Layer叠加可以逼近,但是会显著的增加参数量。
Adder Layer为什么无法逼近恒等映射?
文中的Theorem 1。
描述低分图像Iy和带权重的Adder LayerW的恒等映射:
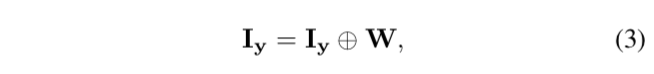
这个等式是不成立的,是因为:
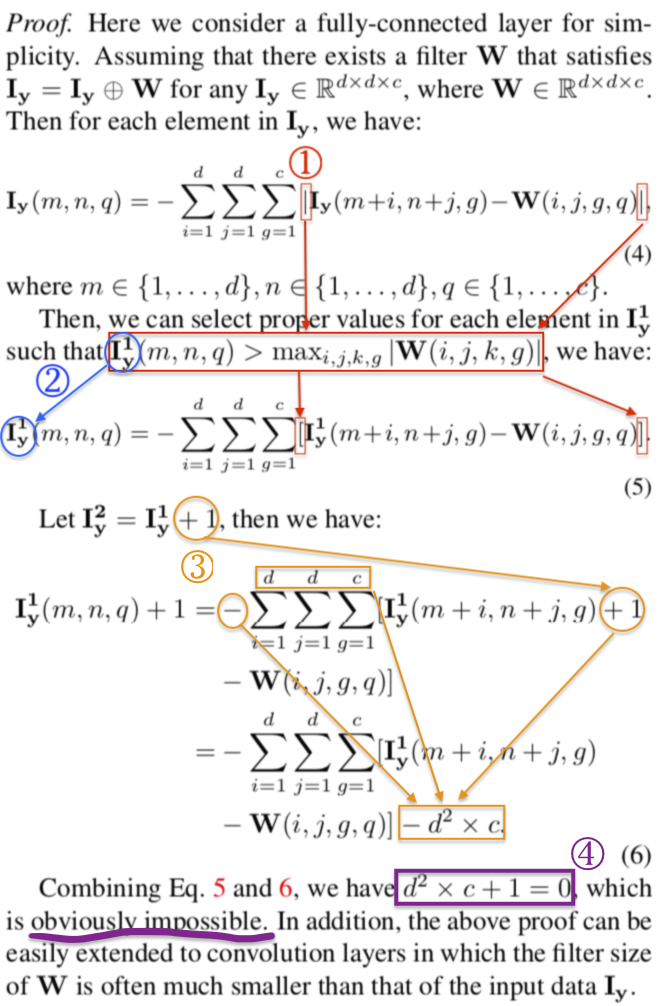
如何实现恒等映射?
改进Adder Layer:为每个Adder Layer增加自快捷操作(self-shortcut operation):
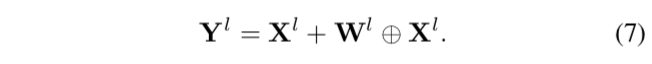
其中Wl是第l层中加法器滤波器的权重,Xl是输入,Yl是输出。
根据式(7),Yl包含Xl本身,则可以通过减小Wl,使等号右边近似等号左边。
与图像识别任务不同的是,大多数SISR问题的特征应该保持一个固定的大小,即Xl和Yl的宽度和高度完全相同。因此,式(7)可嵌入大多数常规SISR模型中。
Learnable Power Activation
自然图像通常由不同的频率信息组成。例如,背景和大面积的草都是低频信息,其中大部分相邻像素非常接近。与此相反,物体和某些建筑物的边缘对于给定的整个图像来说,都是精确的高频信息。
理想的高通滤波器Φ(·)可定义为:
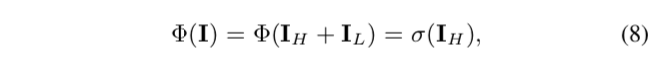
对于卷积操作,高通滤波的实现也很简单,比如:

但是Adder Layer无法实现高通滤波。
Adder Layer为什么无法实现高通滤波?
文中的Theorem 2。
令E ∈ R_d×d 是给定SR模型的输入,其中每个元素等于1。W表示任意Adder Layer的权重。s ∈ R。则不存在W和常数a ∈ R满足以下等式:
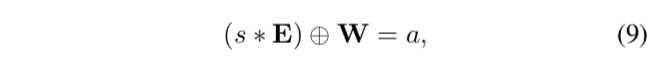
是因为:

如何实现高通滤波?
提出了Learnable Power Activation函数来解决Adder Layer的高通滤波问题和细化输出图像:
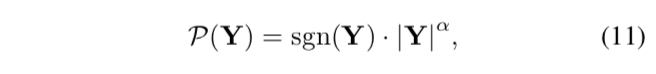
其中,Y为输出特征,sgn(·)为符号函数。
α > 0是一个可学习的参数,用于调整信息和分布。当α > 1,式(11)可以增强输出图像的对比度,强调高频信息;当0 < α < 1,式(11)可以平滑输出图像中的所有信号并去除伪影和噪声。
式(11)可以很容易地嵌入到任何SISR模型的常规ReLU中。
式(11)的背景:Box-Cox变换应用于图像去噪任务中、Box-Cox变换在图像超分辨率中的功能。没有过多解释和证明。
Fortunately, Sharabati and Xi [29] applied the Box-Cox transformation [28] in the image denoising task and found that this transformation can achieve the similar functionality to that of the high-pass filters without adding massive parameters and calculations. Oliveira et al. [26] further discussed the functionality of Box-Cox transformation in image super- resolution. In addition, a sign-preserving power law point transformation is also explored for emphasizing the areas with abundant details in the input image [27].
实验
实验具体细节不放了,直接放数据:

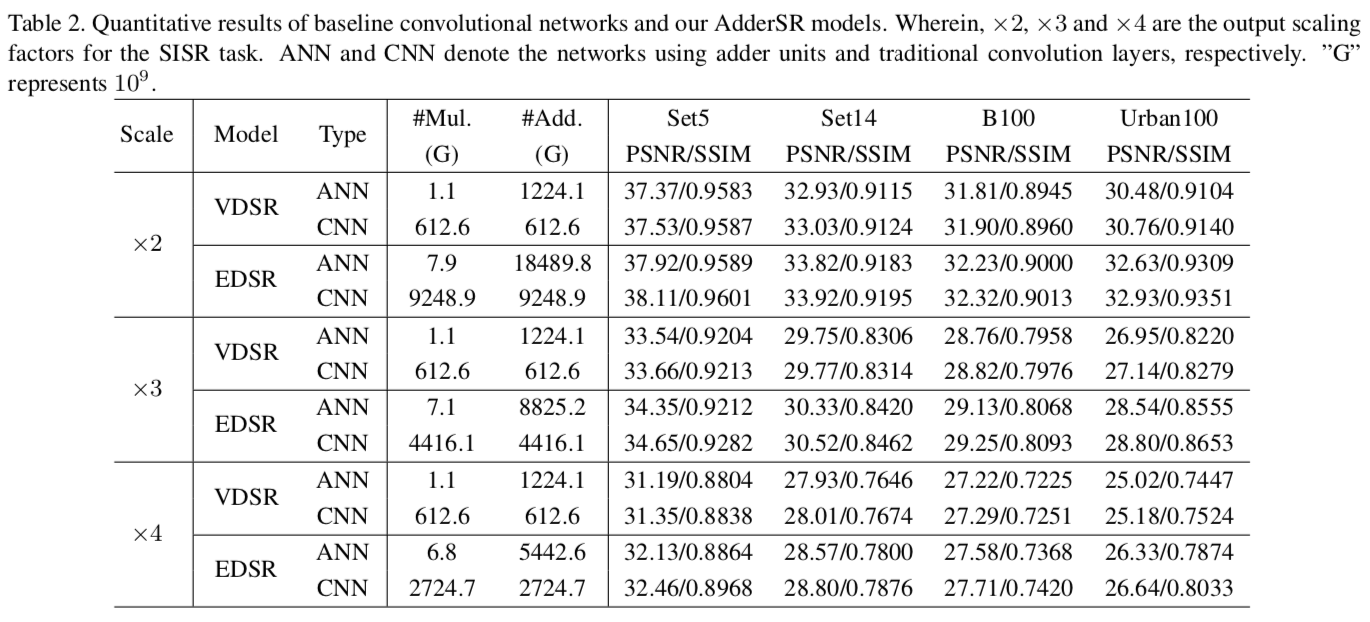
做出来的3倍的效果:

其他
code:上一个工作的拓展,所以和上一篇的code放在一起了。
感想
最大的问题还是实验部分没有提速度,这本来是一个加速的工作,不提速度只说工作量,确实有点问题。
评价指标结果相当相当接近CNN了,这方面真的很厉害。
其他
卷积、互相关、自相关
卷积的数学表示:
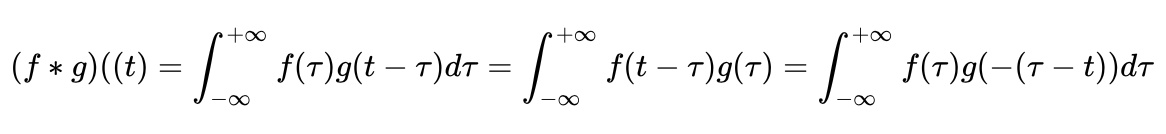
互相关的数学表示:
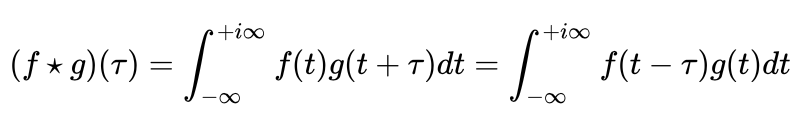
互相关的公式中,变量和积分对象不再是t,而是tao。也就是说互相关研究室的是两个对象产生一段时间差tao之后的关系,也就是相不相关,如果平移之后两个函数正交,那么他们就没有相互关系,互相关为0。
如果tao是偶函数的话,互相关与卷积的结果是一样的。
卷积、互相关与自相关 - 知乎专栏
https://zhuanlan.zhihu.com/p/62292503
L1距离/L1-norm
L1-norm又叫做taxicab-norm或者 Manhattan-norm,可用在曼哈顿区坐出租车来做比喻。图中绿线是两个黑点的L2距离,而其他几根是L1距离。
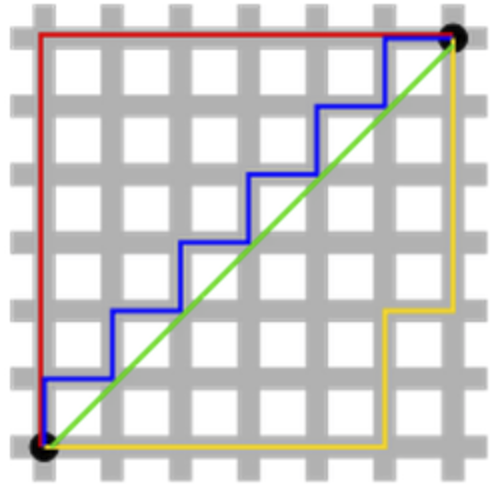
理解L1,L2 范数在机器学习中应用 - 简书
https://www.jianshu.com/p/6cf5d60db634
signSGD
SIGNSGD: compressed optimisation for non-convex problems
文章核心是:SGD里面,梯度真正有用的是方向而不是大小。所以,即使只保留梯度的符号来对模型进行更新,也能得到收敛的效果。甚至有些情况下,这么做能减少梯度的噪声,使得收敛速度更快。
根据上面的结论,进而衍生出了三种算法。SignSGD是第一种:直接把gradient求sign:

SignSGD 及其 MXNet 实现解读 - 知乎专栏
https://zhuanlan.zhihu.com/p/112346480
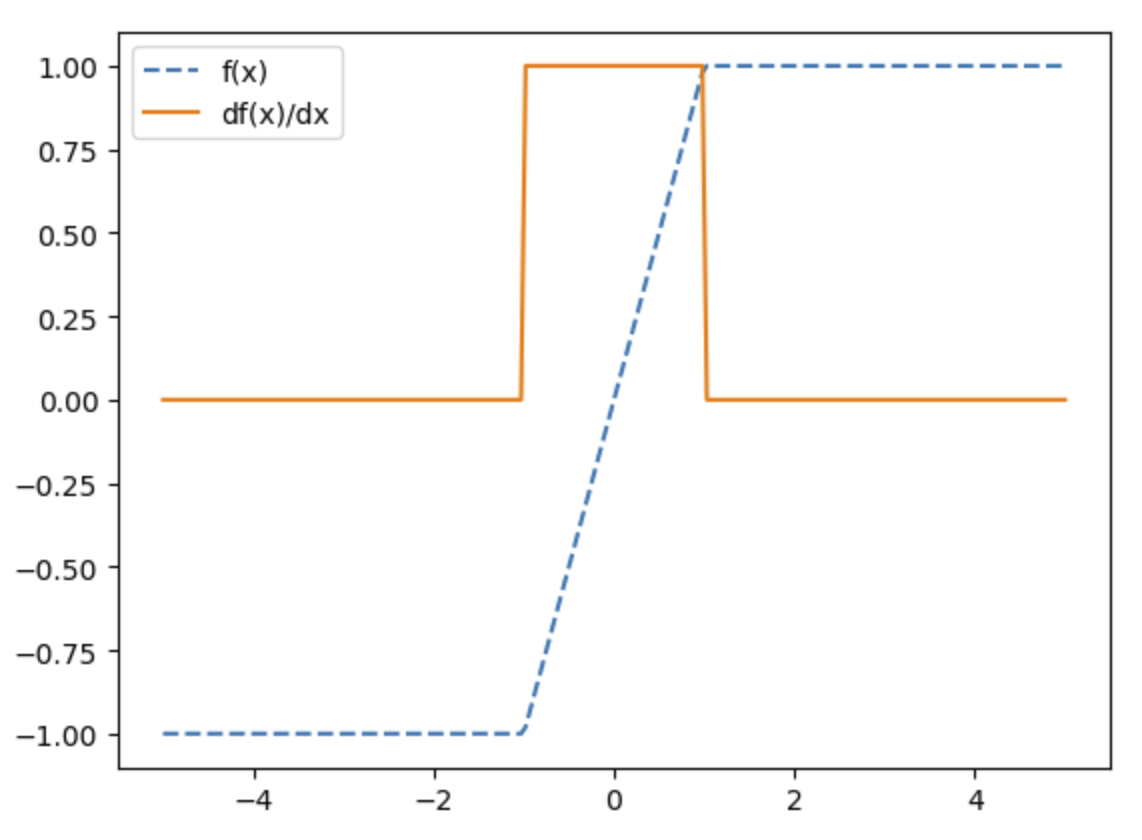
HardTanh
HardTanh比Tanh计算开销小,缺点是和dying relu类似,部分参数可能不更新。
文章中的公式:
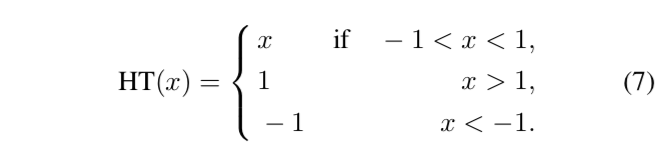
图像:
Identity Mapping
Identity Mappings in Deep Residual Networks
2016 ECCV
这个关键词何凯明大佬为了残差网络而提到的。这篇文章的核心是:分析了残差模块的传播方式,能过解释为什么使用identity mapping作为跳跃连接和加和的激活项,能使得前向和反向的信号能直接在模块之间传播。
Box-Cox变换
是Box和Cox在1964年提出的一种广义幂变换方法,是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。
Box-Cox变换之后,可以一定程度上减小不可观测的误差和预测变量的相关性。
box-cox变换 - 百度百科
https://baike.baidu.com/item/box-cox变换/10278422?fr=aladdin
